Topic DPL: Derivations in predicate logic

2 More derivations

So far you have learned two of the four
quantifier rules. In this section you will
learn the other two rules for the quantifiers.

2.1 Universal Quantifier Introduction

Universal Quantifier Introduction permits you, in
certain circumstances, to add a universal quantifier
to a derivation. For example,

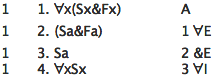
This shows ∀x(Sx&Fx) ∀xSx .

Here is a statement of ∀I:

∀I (Universal Quantifier Introduction)
For any variable v and constant c,
if you have derived φv/c, and c does not occur in φ,
and c does not occur in anything φv/c depends on,
and ∀vφ is a well-formed formula of MPL,
then you can write down ∀vφ,
depending on everything φv/c depends on.

This may look a little complicated at first, but once
you see the reason it is written that way, you will
find it no more complicated than the quantifier rules
you have learned already. Suppose you have written
down φv/c in your derivation. If you want to write
down ∀vφ using this rule you need to satisfy three
restrictions. The first restriction is that c does not occur
in φ. The second restriction is that c does not occur in
anything φv/c depends on. The third and last restriction
is that ∀vφ be a well-formed formula of MPL.

Let's think about why these restrictions are built
into the rule.

If the third restriction was not present, then the
following would be a correct derivation:

The expression on line 2 is not a
well-formed formula of MPL. One of the goals
of our system is to make sure that each of the
rules of our system is sound, that is, at each line
in our derivation you write down a formula which
is entailed by its dependencies. If you could
write down line 2 we would have failed to achieve
one of the goals of our system.

Exercise 2.1a
Some natural deduction systems permit you to write
down expressions which are not well-formed formulas.
Can you think of any reason why this might be a
good idea?

The second restriction on Rule ∀I is that the c
does not occur in anything φv/c depends on.
If that restriction was not present, Rule ∀I would
not be a sound rule. It is easy to see why:

"Fa" does not entail "∀xFx". So the formula on
line 2 is not entailed by its dependencies.
If you could use Rule ∀I to write down line 2,
then Rule ∀I would not be sound. Rule ∀I does
not permit you use line 1 to write down line 2
because "a" occurs in "Fa" and the "Fa" on line 1
depends on "Fa".

Exercise 2.1b

Explain why "Fa" does not entail "∀xFx".

The final restriction on Rule ∀I is that c does not
occur in φ. If this restriction was not present then,
again, Rule ∀I would not be a sound rule:

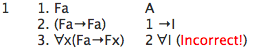
In this example, φ is "(Fa→Fx)", v is "x", c is "a",
and φv/c is "(Fa→Fa)". If Rule ∀I worked this way,
we would be able to show ∀x(Fa→Fx) even though
it is not the case that ∀x(Fa→Fx). Thus, if
Rule ∀I worked this way, it would be unsound.

Exercise 2.1c

Explain why line 3 in the last example violates Rule ∀I.

Exercise 2.1d

Show that it is not the case that ∀x(Fa→Fx).

2.2 Existential Quantifier Elimination

Now for the last quantifier rule, existential
quantifier elimination. Here is an example:

Rule ∃E permits you to derive things when you
have an existentially quantified formula as in
"∃x(Sx&Rx)" on line 1. To use the rule,
you assume an instance of the existentially quantified
formula and then derive something from it. In this case
"(Sa & Ra)" is assumed and "∃xSx" is derived from it.
At this point Rule ∃E lets you write down what you
have just derived a second time, changing its dependencies.
While line 4 depended on the assumption
in line 2, the rule lets you write down the same formula
depending on the existentially quantified formula in line 1.

In essence, the idea behind of the rule is this:
when an existentially quantified formula like "∃xFx" is
true under some interpretation, then you know
that at least one formula like "Fa" or "Fb" or
"Fc" or (and so on) is also true. But you don't know
which one. Still, what you can do is assume one of
these formulas (such as "Fb") and try to show
something that you could show whether you
assume "Fa" or "Fb" or "Fc" or whatever.
For example, in the derivation above, we assumed
"(Sa & Ra)" to derive "∃xSx". But we could have
just as well assumed "(Sb & Rb)" or "(Sc & Rc)" etc.
The choice of the constant didn't matter in
deriving "∃xSx". That shows that "∃xSx" follows
not only from "(Sa & Ra)", but from
"∃x(Sx&Rx)" as well.

Here is the rule, with all its restrictions:

∃E (Existential Quantifier Elimination)
For any variable v and constant c,
if you have derived ∃vφ, assumed φv/c, and derived ψ,
and c does not occur in ψ, φ, or anything ψ depends on (except φv/c),
then you can write down ψ a second time, depending on everything
the first ψ depends on (except the assumption φv/c) together with
everything ∃vφ depends on.

Here are two examples of misuse of the rule,
to help see how to use it correctly.

In this last example, φ is "Fx", v is "x",
c is "a", ∃vφ is "∃xFx", φv/c is "Fa",
and ψ is "(Fa & Ga)". The problem here
is that c occurs in ψ on line 4
("a" occurs in the formula on line 4).
So Rule ∃E cannot be used this way at
line 5.

Here is another example of an incorrect
use of the rule:

To be sure, this example is not correct,
otherwise you would be able to show
that if something is fat, then everything is fat!

Exercise 2.2a
What restriction of the rule is violated
on line 3 of the last example?

2.3 Soundness and completeness

Our MPL natural deduction system is sound.
You can verify this for yourself, by examining
each of the rules to ensure that the rules only
permit you to write down well-formed formulas
which are entailed by their dependencies.
That the system as a whole is sound means:

For any MPL formula φ, if φ, then φ,

and

For any MPL formula φ, and list of MPL formulas X,
if X φ then X φ.

The system is also good for a further reason;
it is complete. That the system is complete means:

For any MPL formula φ, if φ then φ.

and

For any MPL formula φ, and list of MPL formulas X,
if X φ then X φ.


We won't prove completeness of our MPL system
in this introductory course. But it is useful to
know that the system is complete.
In SL you can use the truth table method
to determine whether or not a particular SL formula
is valid. But in MPL you cannot rely on the truth
table method to determine whether or not an MPL
formula is valid. You need some other method.
Since the natural deduction is system for MPL
is complete, if an MPL formula is valid, there is
a derivation of the formula using the system.

Exercise 2.3a
Show that "∀x(Fx→Fx)" is valid in two different ways.

Exercise 2.3b
Suppose you try to find a derivation of a certain MPL
formula, but you do not succeed in finding a derivation.
Does it follow that that formula is not valid?


2.4 Practice

Exercise 2.4a

Show the following:

∀xHx ⊢ Ha
∀xHx, (Hc → ∃xGx) ⊢ ∃xGx
∀x(Hx→Mx), ∀xHx ⊢ ∀xMx
Ha ⊢ ∃yHy
(Ab → Dc) ⊢ (Ab → ∃xDx)
∃x(Fx & Gx) ⊢ ∃xFx
∀x(Fx→∀yGy) ⊢ ∀x∀y(Fx→Gy)
∀x(Px→Qx), ∀x(Qx→Px) ⊢ ∀x(Px↔Qx)
∃x~Px ⊢ ~∀xPx
(∃xPx→∀x(Qx→Rx)), (Pa&Qa) ⊢ Ra
(∀x(Px→Qx)→∃x(Rx&Sx)), (∀x(Px→Sx)&∀x(Sx→Qx)) ⊢ ∃xSx
(∀x(Px&~Qx)→∃xRx), ~∃x(Qx∨Rx) ⊢ ~∀xPx
(∃x~Px→∀x~Qx), (∃x~Px→∃xQx), ∀x(Px→Rx) ⊢ ∀xRx
~∃x(Px∨Qx), (∃xRx→∃xPx), (∃xSx→∃xQx) ⊢ ~∃x(Rx∨Sx)