Topic DPL: Derivations in predicate logic

1 Derivations in monadic predicate logic

Now you will learn a natural deduction system
for Monadic predicate logic.

1.1 The rules are very similar

We adopt versions of the 12 rules from the natural
deduction system for SL discussed in Topics 1 and 2.
While the old rules applied to SL formulas, these adopted
rules apply to MPL formulas. Otherwise, the rules are
unchanged. This provides rules for all the connectives
of MPL.

Additionally, rules for the quantifiers '∃' and '∀' are
needed. For each quantifier, there is an elimination rule
and an introduction rule. With the four quantifier rules,
that makes 16 rules in all.
Here are all of the rules, if you are in a hurry.

Exercise 1.1a

Explain why rule &E for MPL is a sound rule.

1.2 Rule of Existential Quantifier Introduction

The first quantifier rule is the rule of Existential Quantifier
Introduction. Here is this rule in action to show Sa ∃xSx:

Rule ∃I says that you can take a formula you have
written already, replace one or more occurrences of some
constant in the formula with a new variable, and then attach
the existential quantifier to the front. The dependencies of the
new formula are the same as the old formula.

Notice that ∃I is a sound rule. That means that when
you use the rule, the formula you write down is entailed
by its dependencies. Consider the previous example, where
the rule is used at line 2. Note that for any interpretation under
which "Sa" is true, "∃xSx" is true under that interpretation too.

Exercise 1.2a

Explain why for any interpretation under which
"Sa" is true, "∃xSx" is true too.

Here is another example of ∃I in action:

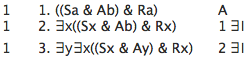
Two details should be noted in using ∃I.
The first detail is that ∃I applies to the whole
formula, not to part of the formula. That means
that the quantifier is added at the beginning of the
formula, not in the middle. Thus, for example,
the following derivation is incorrect:

If you could do this, then rule ∃I would not be sound
because you could write down a formula which is not
entailed by its dependencies. Line 2 is not entailed by
its dependency, line 1. Take an interpretation under
which "Sa" and "Ab" are false, but "Sb" is true. This is
an interpretation under which "(Sa → Ab)" is true and
"(∃xSx → Ab)" is false. So "(Sa → Ab)" does not entail
"(∃xSx → Ab)".

So, remember: when using ∃I, the existential quantifier
must be added to the front of the formula. The following
is an example of a similar, but correct derivation:

Exercise 1.2b

Show (Fa & Ga) ⊢ (∃xFx & Ga)

The second detail to be noted about ∃I
is that that the formula you write down must
be a well-formed formula of MPL. Thus, for
example, the following derivation
is not correct:

The derivation is not correct because the formula
on line 2 is not a well-formed formula of MPL.
The variable 'x' already occurs in line 1, so you
cannot use the variable 'x' in applying ∃I. You need
to choose a different variable. You could, for instance,
use 'y' instead:

In using ∃I you always need to choose a new
variable or the expression you write down
will not be a well-formed formula.

Exercise 1.2c

Explain why "∃x(∃xSx & Rx)" is not a well-formed
formula of MPL.

On the list of rules, Rule ∃I is stated precisely
using some shorthand symbolism:

∃I (Existential Quantifier Introduction)
For any variable v and constant c,
if you have derived φv/c,
and ∃vφ is a well-formed formula of MPL,
then you can write down ∃vφ,
depending on everything φv/c depends on.

This statement of the rule uses the symbolism
"φv/c". This symbolism is a shorthand
which makes it simpler to state the quantifier
rules. As we will be using it, "φv/c" means that
you take an expression φ and replace all
occurrences of v with c. For example,
if φ is "(Fx&Fb)", v is "x" and c is "a", then
φx/a is "(Fa&Fb)". If v is "x" and c is "b"
then φx/b is "(Fb&Fb)".

Exercise 1.2d

State Rule ∃I without the shorthand symbolism.

1.3 Rule of Universal Quantifier Elimination

A second straightforward rule for the quantifiers is
the rule of universal quantifier elimination, ∀E:

∀E (Universal Quantifier Elimination)
For any variable v and constant c,
if you have derived ∀vφ,
then you can write down φv/c,
depending on everything ∀vφ depends on.

This rule is easy to use. For instance:

Or, another example:

However, the following is incorrect:

This is incorrect because line 1 is a conjunction,
not a formula beginning with a universal quantifier.
Since the formula on line 1 does not begin with
a universal quantifier, ∀E does not apply. ∀E only
applies to formulas beginning with a universal
quantifier.

Exercise 1.3a

Explain why Rule ∀E is a sound rule.

1.4 An example

Here is an example of a derivation in MPL using
rules you have learned so far:

This shows (Sb→∀xEx), ~Ea ~∀xSx .

Exercise 1.4 a

Find a shorter derivation showing that (Sb→∀xEx), ~Ea ~∀xSx .