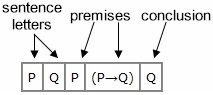
P, (P→Q) QTo prove that it is valid, we draw a table where the top row contains all the different sentence letters in the argument, followed by the premises, and then the conclusion :

Then using the same method as in drawing complex truth-tables, we list all the possible assignments of truth-values to the sentence letters on the left. In our particular example, since there are only two sentence letters, there should be 4 assignments :
| P | Q | P | (P→Q) | Q |
| T | T | |||
| T | F | |||
| F | T | |||
| F | F |
The next step is to draw the truth-table for each of the premise and also the conclusion. First, the first premise :
| P | Q | P | (P→Q) | Q |
| T | T | T | ||
| T | F | T | ||
| F | T | F | ||
| F | F | F |
Then the second premise:
| P | Q | P | (P→Q) | Q |
| T | T | T | T | |
| T | F | T | F | |
| F | T | F | T | |
| F | F | F | T |
Finally for the conclusion:
| P | Q | P | (P→Q) | Q |
| T | T | T | T | T |
| T | F | T | F | F |
| F | T | F | T | T |
| F | F | F | T | F |
In the completed truth-table, the first two cells in each row give us the assignment of truth-values, and the next three cells tell us the truth-values of the premises and the conclusion under each of the assignment. If an argument is valid, then every assignment where the premises are all true is also an assignment where the conclusion is true. It so happens that there is only one assignment (the first row) where both premises are true. We can see from the last cell of the row that the conclusion is also true under such an assignment. So this argument has been shown to be valid.
Question 1 - Note that in the table above the conclusion is false in the second and the forth row. Why can't we say that they show that the argument is invalid?Remember that “(P→Q), ~P, therefore ~Q” is invalid. Verify for yourself that this is the truth-table for the sequent :
| P | Q | (P→Q) | ~P | ~Q |
| T | T | T | F | F |
| T | F | F | F | T |
| F | T | T | T | F |
| F | F | T | T | T |
Check for yourself that the truth-table is done correctly. A sequent is invalid if there is at least one assignment where the premises are true and the conclusion is false. The third row of the table shows that this is indeed the case. When “P” is false and “Q” is true, the two premises are true but the conclusion is false. So the argument is not valid. We call such an assignment an invalidating assignment (a counterexample) for the sequent.
So far we have only looked at sequents where each WFF contains at most one sentential connective. Now let us look at sequents with more complex WFFs, such as this one here :
(~P∨Q), ~(Q→P) (Q↔~P)Again we draw a truth-table for the premises and the conclusion :
| P | Q | (~P∨Q) | ~(Q→P) | (Q↔~P) |
| T | T | FT T T | F T T T | T F FT |
| T | F | FT F F | F F T T | F T FT |
| F | T | TF T T | T T F F | T T TF |
| F | F | TF T F | F F T F | F F TF |
Question 2 - For any three formula φ1, φ2 and φ3, if φ1 φ2, and φ2 φ3, does it follow that φ1 φ3?Examine this table and answer the questions:
P Q ~Q (P↔Q) ~P T T F T F T F T F F F T F T F F F T T T Which sequent is being tested for validity in this table?
Is the sequent valid according to this table?
There are two mistakes made in this table. Can you identify them?
Question 3 - Use the full truth-table method to determine the validity of these sequents:
Question 4 - For any two formula φ and ψ, if φ ψ, does it follow that ψ φ?Question 5 - For any two formula φ and ψ, if φ does not entail ψ, does it follow that ψ entail φ?
Question 6 Confirm for yourself that the WFFs in each pair of WFFs below are logically equivalent to each other :
What is interesting and perhaps surprising is that decidability no longer obtains when we are dealing with some more powerful systems of logic. One of the most important discoveries in modern logic is that mathematics is undecidable. In particular, Gödel's first incompleteness theorem says that there any consistent systems of mathematics would have to include statements that can neither be proved or disproved. In other words, it is impossible for there to be a computer program that can tell whether these statements are true.