Topic DS: How to prove things with Sentential logic

1 Derivations in sentential logic

Now you will learn how to make derivations in sentential logic.
A derivation displays step by step reasoning from premises
to conclusion. Each step along the way follows the rules.
The sort of system of rules you will study is often called a
natural deduction system because it is somewhat like the
way people actually deduce conclusions from premises. It
isn't really natural---it is an artificial, formal system---
but a natural deduction system can be easier to use and
understand than other available methods.

1.1 An example derivation

Here is an example of a derivation in our system:

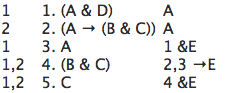
This example shows, step by step, that "C" follows
from "(A & D)" together with "(A → (B & C))".
That is, starting with "(A & D)" and "(A → (B & C))"
one can reach the conclusion "C" by following the
rules of the system. In short, "C" is derivable
in our system from "(A & D)" and "(A → (B & C))".
In symbols:

(A & D), (A → (B & C)) C

The symbol "" is sometimes called the "turnstile".
We will use it to mean that the formula on the right
is derivable in our natural deduction system from
the formulas, if any, on the left.

1.2 The parts of a derivation

Let's examine the sample derivation in detail.

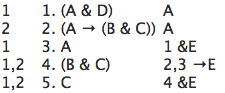
The middle column is a numbered list of well-formed
formulas of sentential logic. This is the heart of the
derivation. Each formula in the list is numbered.
In this case there are five formulas, numbered
from 1 to 5.

The right column tells us what rule is followed.
In this derivation three different rules are used.
In line 1 "(A & D)" was written down by Rule A,
the Rule of Assumption. The Rule of Assumption
is also used on line 2. On lines 3 and 5 Rule &E
is followed, and line 4 employs rule →E. There are
twelve different rules in all in our system.

The left column contains a list of zero or more
dependencies. For example, line 1 depends on line 1,
and line 5 depends on lines 1 and 2. We'll see more
about what the dependencies mean as we go along.

In short, at each step in making a derivation you
write down three things: a formula (with a line number),
a note on the right saying which rule you have applied,
and, on the left, a list of dependencies (if any).

1.3 Three rules

You have just seen three rules in action. Let us see
more precisely how to use each of these three rules.

The Rule of Assumption says that you can write
down any well-formed formula of SL you like.
The dependency is that formula itself.
For example, we just saw this rule used twice:

It may seem odd to be able to write down any formula
you want at any time. But that does not mean you can
derive anything at all. The rule does not merely say you
can write down any formula. The rule says that you can
write down any formula depending on itself.
In effect, for any formula φ, the rule lets you say that
φ follows from itself; φ is derivable from itself.
In this case, for example, line 1 means that "(A & D)"
is derivable from "(A & D)":

(A & D) (A & D)

And line 2 means that "(A → (B & C))" is derivable
from "(A → (B & C))":

(A → (B & C)) (A → (B & C))

The & Elimination Rule, &E, says that if you have
a line which is a conjunction you can write down
either of the conjuncts. In other words, if you
have a line (φ&ψ), you can write down φ or ψ.
The new line depends on everything the conjunction
depends on.

That rule is used at line 3 of the sample derivation:

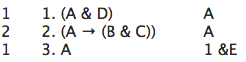
One can use &E to write down "A" at line 3 because
line 1 is a conjunction, "(A & D)". Line 3 depends on
everything line 1 depends on. Line 1 depends only
on line 1. So line 3 depends only on line 1.
The annotation on the right says that you applied
&E to line 1.


The → Elimination Rule, →E, says that you can
write down ψ if you have a line (φ→ψ) and another line φ.
The new formula ψ depends on everything that (φ→ψ) depends
on, together with everything that φ depends on.
This rule is commonly called Modus Ponens.
But we call it the → Elimination Rule to emphasize the
similarity between this and other elimination rules,
such as &E. Using an elimination rule, one writes down
part of an earlier formula. So elimination rules let one
move from longer formulas to shorter formulas.


→E is used at line 4 of the sample derivation:

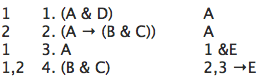
In this case, we have "A" on line 3,
and "(A → (B & C))" on line 2, so we can
write down "(B & C)", depending on
everything line 2 and line 3 depend on.


1.4 Practice Exercises

Now you have seen 3 rules: &E, →E, and A.
It is time to prove some things yourself!
Make derivations to show the following,
using only these 3 rules, if you can.
Try not to look at the answers
until you have finished your derivation,
or have decided that it can't be done.

Exercise 1.4a

Show the following using only &E, →E, and A.

(A & B) A

((A ∨ B) & (B→A)) A

(A → (B & C)), A B

A, B (A & B)

A, (A → (B → (C → (D → (E → F))))) F