Philosophy of the Sciences, 1997
Meeting 13: Quantum Theory I
Summary
1. On the atomic scale, things like motion,
energy and spin do not exhibit continuous variability, but are discrete
or (in Paul Davies' word) `lumpy'. This immediately raises an enormous
problem. Classically, the dimensions for energy include distance
and distance-over-time (velocity). Since distance and velocities
are continuous quantities then so is classical energy. So, to be
told that, at the atomic level, energy is non-continuous is puzzling.
One is immediately inclined to say `Are we talking here about two entirely
different concepts which, accidentally as it were, share a name ?'.
If the meaning of a theoretical term is a function of the theory in which
it is embedded, should we say that the two concepts of energy are
incommensurable ? If so, then there would be no possibility of comparing
the embedding theories directly with each other. Could we compare
them by seeing how well each squares with the facts ? One problem
is that we don't have access to the facts other than via how we describe
or conceptualize them, so we may sometimes have no way of representing
the facts which is neutral between competing theories. Another problem
is that, especially since the advent of quantum theory, many physicists
have been suspicious of the notion of the facts or of reality
(see Peierls interview [reading list]). We shall
try to assess whether such suspicion is justified.
go to summary
2. At the very beginning of this century,
solutions to certain recalcitrant problems, such as black body radiation,
were found, and these solutions depended on the postulation of electromagnetic
radiation in the form of indivisible, discrete packets of energy. By means
of quantum mechanical equations we can calculate the intensities and frequencies
of spectral lines. The notion of electron spin in Dirac's formulation
of relatavistic quantum mechanics furnishes a theoretical understanding
of what had previously seemed inexplicable phemonena like magnetism and
chemical bonding. We can also now answer Lord Kelvin's question of
how the atoms of a solid body are held together, and can explain properties
such as electrical conductivity and superconductivity. Einstein in
1905 gave a satisfactory quantum theoretic explanation of the photoelectric
effect [light falling on a suitable surface produces electric current]
and since then similar explanations have accounted for many of the interrative
processes between radiation and material objects -- the Compton effect
[an X-ray scattered from a free electron changes in wavelength] , the phenomenon
of dispersion etc.. Even the existence of such initially puzzling
entities as antiparticles are rendered intelligible by means of the concepts
of quantum theory. We may say, then, with little hesitation, that
quantum theory is an extremely well-confirmed scientific hypothesis --
or, in Popperian terms, that it has not been falsified and is corroborated
to a very high degree.
3. In the early nineteenth century, experiments
had conclusively shown that light (like sound) consists of waves
spreading from a source. The answer seems to be that photons have
a dual character: light waves are particulate. From 1913 onwards,
the idea gained ground that, conversely, matter (particles) is wave-like.
The explanation given for the orbiting of electrons at only certain fixed
energy levels (as required by Bohr's theory) was that electrons, like photons,
have wave-like characteristics, and the discreteness of the energy levels
corresponds to the possibilities of patterns of standing (stationary) waves
around the nucleus. Newton's mechanics and Maxwell's laws of electrodynamics
cannot cope with these phenomena, and a new theory known as quantum mechanics
was developed in the 1920s by Schrödinger and Heisenberg and further
elaborated by Dirac, Fermi, Born and others. As Davies and Brown
point out (p.4), no known experiment has contradicted the predictions of
quantum mechanics in the last 50 years, and, as we saw, the theory has
offered explanations of numerous phenomena that were previously not understood.
go to summary
4. Philosophical problems arise, however,
when the question is raised of just how the quantum theory is to be interpreted.
The trouble is that the theory seems to demand that the microphenenomena
be wavelike for the purposes of some explanations (like that of interference)
and particulate for the purposes of some other explanations (like that
of the photoelectric effect). Now we are all familiar with the controversy,
stemming from the 17th century debate between Newton and Huyghens on the
nature of light, with Newton advocating the corpuscularian theory and Huyghens
the wave theory. A presupposition of this controversy is that being
particulate and being wavelike are incompatible properties. And this
seems an entirely reasonable presupposition. A particle is, after
all, a discrete object which occupies a precise spatial position at any
one time, whereas a wave is a spreading undulation. But according
to the interpretation of quantum theory now favoured by most physicists
the wave picture and the particle picture are not incompatible, but are
complementary. This interpretation, known as the Copenhagen
Interpretation, links Bohr's principle of complementarity with the Uncertainty
Principle developed by Heisenberg [(indeterminacy in position x indeterminacy
in momentum >= h/2) where h is Planck's constant and m
the mass of the particle.] According to Heisenberg the Copenhagen
Interpretation received its crucial test in the autumn of 1927 at the Solvay
Conference in Brussells and emerged, in this opinion and that of the majority
of physicists, successful.
go to summary
5. Suppose a beam of polarized light
is incident on a polarizer. Then the intensity of the transmitted
light is some fraction of that of the incident light determined by the
angle between the plane oft the polarization of the incident light and
that of the material. Now suppose the intensity of the incoming beam
is reduced to one photon at a time. Then, in accordance with the above
result, only a proportion of photons will pass through. But,
given that all photons are identical, why should one pass through but not
another ? We can onlyionhall conclude that it is a random matter.
6. It is important to notice that, in the above discussion, no
mention has been made of an observer. We have said that some physical
behaviour is random, and this is quite different from saying that
it is unknown by us. Whereas classically all of nature was believed
to be subject to the deterministic laws of causality (Laplace), in quantum
theory nature itself is ascribed an indeterminacy. The Heisenberg principle
is misleadingly named the `uncertainty' principle. As Davies and
Brown stress (p.7), the electron itself does not possess both a
position and a momentum simultaneously -- this is something inherent in
nature. Of course, it follows trivially from this that we
cannot be certain of both an electron's position and momentum at any one
time.
go to summary
7 The intrinsic randomness is, again demonstrated
through Young's slit apparatus. Consider a point source S which emits
electrons. There is a crystal lattice L containing two slits numbered
1 and 2 and behind L there is a fluorescent surface F.
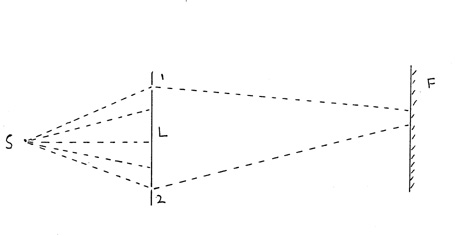
Reduce the intensity of the source to a stream of single photons. After
passing through one or other slit, the photon hits a definite point on
the screen and leaves a mark. These marks gradually accumulate to form
the pattern of bright and dark `interference fringes'. Initially, you may
not find this puzzling. For we are all familiar with those experiments
in which coins fall under gravity through rows of equispaced nails.
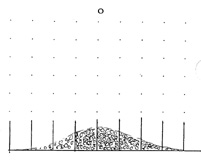
Here each coin follows an apparently random route, yet cumulatively
we get the familiar distribution curve.
8. One thing that is puzzling about the Young's
slit situation is not that we get a pattern out of the individual scintillations,
but the precise pattern that we get. For that pattern is the wave
interference pattern. When one slit, say number 2, is closed, and radiation
of very low intensity is emitted then we observe individual and flashes
-- minute scintillations on a particular area of F. Suppose we we
tried to explain this on the wave theory. We should say that spherical
waves leave S, pass through Slit 1, setting up a secondary wave system
centred at slit 1. So waves from Slit 1 are hemispherical.
But when such a wave strikes F, a flash is produced at only one point.
Thus we should have to say either that the wave collapses to a point or
that the wave disappears at all other points. Neither alternative
is acceptable. Each constitutes what Reichenbach called a causal
anomaly -- a statement which that `contradicts the laws established
for observables'.
9. But that's not all! If we do block one of the apertures,
then we no longer get the interference pattern. Here a contrast
with the falling coins demonstration becomes sharp. It would be as
if removing all the nails on the right side resulted in a distribution
like this:
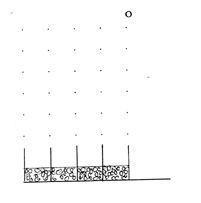
We could put it like this: when both slits are open, a photon passing
through slit A `knows' that it has to contribute to the interference pattern,
but, when slit B is closed, a photon passing through A knows that it has
no such obligation. Therefore a photon passing though A must somehow
`know' about the state of the other slit. This is extremely perplexing.
Suppose a given particle is on the verge of entering slit A, but that the
decision on whether or not to close B is left until the very last instant.
It seems that the behaviour of the particle will be affected by the state
of slit B even though information about that state does not have time
to reach that particle (given that the upper limit for the speed of transmission
of information is set by the speed of light).
10. Phenomena such as these may lead us to wonder what electrons
really are, since they seem to behave in ways that we cannot picture.
According to a widely accepted interpretation of QM (Bohr's) such questions
are illegitimate or meaningless. Physics can make predictions, i.e.,
it can say what effects will result from a given set-up, but it cannot
tell us what is, i.e. it is ontologically non-committal. Properties,
the co-existence of which is contadictory are regarded by Bohr as complementary
since they can never be observed simultaneously. This `Copenhagen
interpretation' is often cited as instancing a positivistic conception
of science, the point being that it accepts statements about observations,
but discards as meaningless or `metaphysical' any statements about underlying
reality, about where electrons really are (independent of observation)
etc.. There are many scientists, notably Einstein, and many philosophers
(e.g. Popper) who reject this interpretation (Popper, echoing Hamlet, says
that it indicates something rotten in the state of Denmark). Opponents
claim that the alleged indeterminacy is not a feature of nature, but merely
a reflection of our ignorance about what `hidden variables' are responsible
for the anomalous results. These opponents seek to restore a common-sense
view of reality, i.e. of a world which exists independently of any observers,
where all events occur because they are caused. As Davies and Brown
nicely put it (p.13) `that ultimately a classical world of familiar cause
and effect underlies the madhouse of the quantum'.
go to summary
11. This opposition of opinions recapitulates
a long-standing philosophical debate. As Martin Gardner explains,
`the question of whether the future is completely determined by the present,
or whether elements of pure chance underlie "being" is one of the oldest
questions in philosophy. It was constantly debated by the ancient
and the medievals. The Greek atomists injected randomness into
the basic structure of the universe by introducing a random "swerving"
of the particles on a level too small to be seen. Lucretius has a
beautiful metaphor on this. He speaks of a flock of sheep moving
about at random on a hill. But, to a distant viewer, they appear
as a white that is motionless. Jumping to recent times, Charles Peirce,
America's greatest philosopher, firmly believed (before QM) that pure chance
was an element in the evolution of the cosmos. He called his view
"tychism". It had a major influence on William James. Note
also that this old metaphysical question is far from settled today.
Many QM experts, Bohm for example, believe (with Einstein) that QM is incomplete
and that when a deeper level is discovered, determinism also will be restored.'
(Physics and Society 19/1, January 1990, p.2)
GO BACK TO COURSE
OUTLINE



