Topic DS: How to prove things with Sentential logic
2 Some rules
In
section DS01
you learned three rules. This section
and the next describe the remainder of the rules of
our system. There are 9 more rules, for a total of 12
rules in all.
If you are impatient, here is a list of
all of the rules.
At this point, there won't be much discussion about
why the rules are the way they are, or whether the
rules should be the way they are. We'll get to that in
Topic RS. For now, just work on learning what the
rules are, and how the rules work.
2.1 Rules for '&'
The
conjunction elimination rule, &E was mentioned
earlier, in
section DS01.
Let us state this rule carefully.
&E
(Conjunction Elimination)
If you have derived (φ&ψ),
you can write down
φ or
ψ,
depending on
everything (φ&ψ)
depends on.
According to this rule, if one of the lines of a derivation
is
a conjunction, (φ&ψ),
then you can add a new line which is
φ
or you can add a line which is ψ.
The greek letters 'φ'
and
'ψ'
stand for any well-formed formula of sentential logic.
Note that the dependencies of the new line are just the
same
as the dependencies of the original line. That is what the
rule
means when it says that the formula you write down depends
on "on everything (φ&ψ)
depends on."
&E helps you simplify things. You can eliminate the
symbol
'&' and write down only part of a formula. That is why
&E
is called an "elimination" rule.
But sometimes you might not want to eliminate '&', but
to add it into a derivation. Sometimes you might want to
write down a formula which contains a '&' when that
'&'
wasn't there before. There is a rule for that:
&I
(Conjunction Introduction)
If you have derived
φ and
ψ, you can write
down (φ&ψ),
depending on everything
φ and
ψ depend
on.
For most of the connectives, the rules in the system come
in pairs like these rules for '&'. There is an
elimination rule,
and an introduction rule. The elimination rule lets you get
rid of a symbol, and the introduction rule lets you add a
symbol when the symbol was not there before.
Rule &I says that if one of the lines of a derivation
is φ
and
one of the lines in the derivation is ψ
then you can add a
new line which is their conjunction: (φ&ψ).
The dependencies
of the new line are the same as all of the dependencies for
the line with φ
put together with all of the dependencies for
the line with ψ.
Here are two brief examples:
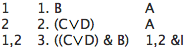

Exercise
2.1a
Is this a correct derivation?

Exercise 2.1b
Show (A & B) ![]() (B & A).
(B & A).
Exercise 2.1c
How many lines are there in the longest
derivation in our system?
2.2
Rules for '↔'
The
rules for '↔'
are straightforward. Here is an example
of a use of the biconditional elimination rule:
![]()
And, unsurprisingly then, here is the introduction rule:
![]()
Thus
↔E
lets you change a biconditional into the
conjunction of two conditionals. And
↔I
lets you
move in the opposite direction. The dependencies
work just as they do for &E: the new dependencies
are the same as the old dependencies. For both
↔E
and
↔I,
you just write down the same dependencies
as before.
Stated explictly:
↔I
(Biconditional Introduction)
If you have derived ((φ→ψ)&(ψ→φ)),
you can write down (φ↔ψ),
depending on everything ((φ→ψ)&(ψ→φ))
depends on.
↔E (Biconditional
Elimination)
If you have derived (φ↔ψ),
you can write down ((φ→ψ)&(ψ→φ))
depending on everything (φ↔ψ)
depends on.
You have now seen half of the rules in the system:
&I, &E, A, →E,
↔E,
and
↔I.
We will get to the
rest of the rules in a moment. But first, you
should try deriving a few things.
Exercise
2.2a
Show the following:
(A
↔
B), (B & C) ![]() A
A
(A →
A) ![]() (A
↔
A)
(A
↔
A)
(A
↔
B), (B
↔
C), A ![]() C
C
2.3
Rules for '→'
and the Rule of Assumption
Rule
→E was introduced in
section DS01:
→E
(Conditional Elimination or Modus Ponens)
If you have derived (φ→ψ)
and φ,
you can write down ψ,
depending on everything (φ→ψ)
and φ depend on.
Sometimes a rule like →E is called, using a Latin
expression,
Modus
Ponens.
But we'll just call it
Conditional Elimination,
or
→E
for short. An example of a use of such a rule in English
would be:
If John has measles then Harry has measles.
John has measles.
Therefore, Harry has measles.
As this seems clearly to be an example of good reasoning,
you can see why we might like to have version of this rule
in
our logical system.
The introduction rule, →I, is a little different from the
other rules
you have seen. One important difference is that →I permits
you
to
decrease
the number of dependencies.
Consider this short example showing B ![]() (A → (A&B)).
(A → (A&B)).

Notice that dependency of line 4 is only line 2,
while line 3 has two dependencies: line 1 and line 2.
Applying the rule →I yields the conditional on line 4
depending on everything line 3 depends on
except
line 1.
Since line 3 depends on 1 and 2, line 4 depends on just 2.
The idea behind →I is that if you can show ψ
given an
assumption φ,
then you have shown that if φ
then ψ,
that is (φ→ψ).
Here is the rule stated explicitly:
→I
(Conditional Introduction)
If you have assumed φ, and you have derived ψ,
you can write down (φ→ψ),
depending on everything ψ depends on except φ.
Rule →I provides a powerful, direct way to derive
a conditional, (φ→ψ).
You simply assume φ
and then,
using that assumption try to derive ψ.
If you succeed,
you will have thereby shown (φ→ψ).
And this conclusion
will no longer depend on the assumption
φ.
Assuming
φ
was just a temporary measure.
One point to keep in mind. Rule →I applies when
you have
assumed φ
and
derived ψ.
Be careful:
assuming and deriving are not the same. You have
derived a formula when it is a line of the derivation
you are working on. You have assumed a formula
when it is written down in your derivation using the
Rule of Assumption. The Rule of Assumption was
explained in section DS01. Here it is again:
A (Rule of
Assumption)
You can write down any SL wff, depending on itself.
Exercise 2.3a
Can you give an example of a derivation where
you assume a formula which you have not derived?
Exercise
2.3b
Is this a correct derivation?

Exercise 2.3c
What is wrong with the following derivation?

Exercise 2.3d
Show
the following:
(P → (Q → R)) ![]() ((P
→ Q) →
(P
→ R))
((P
→ Q) →
(P
→ R))
![]() (A→A)
(A→A)
![]() ((A&B)→A)
((A&B)→A)