[H20] 統計與圖表
日常生活和工作中很難避免接觸到統計數據和圖表。科學研究中,統計更是重要。在這裡我們簡單介紹一下一些有關統計的基本概念和常見陷阱。
§1. 圖表
圖表不只是外觀上比起密密麻麻的數字吸引人注意,而是在很多時候有助於概括(summarize)大量的數據集合(data set)、把重點放在數據的某一方面(aspect)或明顯表現出數據在某段時間上的趨勢(trend)等等。
好的圖表使人立刻觀察到(單從數字上難以明顯察覺到)一個數據的特徵。同樣,差的圖表亦能令人很快得出「表」裡不一的錯誤結論,下面是一些此類圖表的例子:
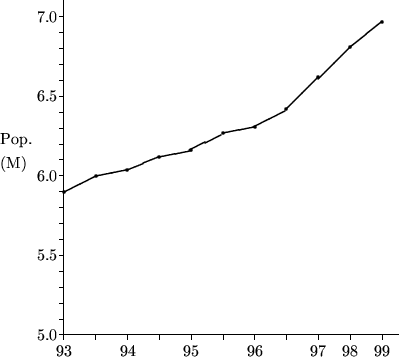
這個關於香港人口數目的折線圖有兩個毛病:
- 根據Y軸上的數字,人口在1993至1999年間增加了18%,但由於1999年的數據點之高度大概是1993年的兩倍,因此有可能在視覺上令人誤以為增幅是100%。此毛病的原因在於沒有明顯讓讀者察覺Y軸的最低點不是由「0」開始,而正確的做法一般是將Y軸之起始部分繪畫成上下起伏的波紋(見例二的線形圖)。
- X軸的比例(scale)不一致。X軸由1993年年頭至1996年年尾以一個間距代表6個月,但對餘下的年份改為以一個間距代表12個月。即使人口增長的情況自1997年起和前期的差不多,該段折線的斜度會是前段的兩倍,以致視覺上令人誤會人口突然大幅上升。
按:上圖是根據政府統計處所提供的人口數據繒成,當局並無發布此圖。
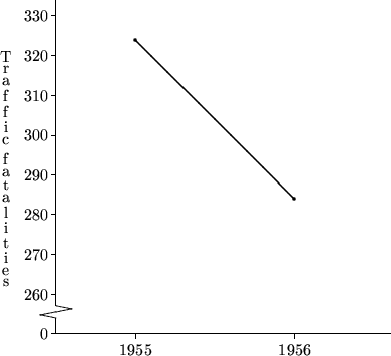
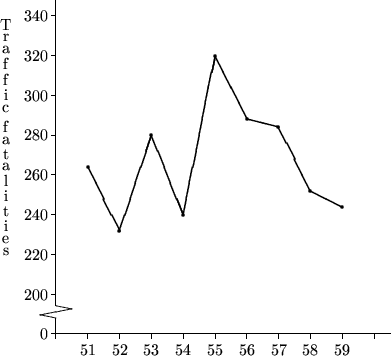
可見在打擊措施推行之前的1951至1952年以及1953至1954年也曾出現過死亡數字的大幅下降(甚至比1956至1957年的大),因此1656至1957年的改善可能只屬每年都有的自然改變。只得兩個數據點的線形圖未必能夠反映事實的真相。
按:上圖的數據來自Donald T. Campbell, "Measuring the Effects of Social Innovations by Means of Time Series" in Judith M. Tanur et al., eds. (1989), Statistics: A Guide to the Unknown. Pacific Grove, CA: Wadsworth,另外裡面對該個案的問題有更詳盡的探討。
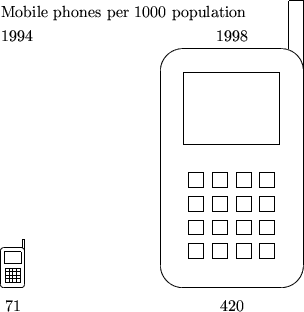
此圖描述了在1994到1998年間香港人擁有流動電話之增長情況。由於數字上(1994年的「71」和1998年的「420」)是增加了6倍,所以右圖的高度為左圖之6倍是正確的繪畫方式,但同時右圖的闊度為左圖的6倍便變成錯誤,因為右圖的面積最終等於左圖之6 × 6 = 36倍,導致視覺上會令人誤解為有36倍的增長。
按:上圖是根據政府統計處所提供的數據繒成,當局並無發布此圖。
§2. 平均數與中位數<
除了用圖表之外,數據很多時都用數字去概括,而最常提及到的統計數字是平均數(mean)。一個擁有N個數字的集合之平均數就是該集合全部數字的總和除以N。例如數據集合 {2, 5, 5, 8, 10} 的平均數是 (2+5+5+8+10) ÷ 5 = 6。
平均數並非表達一個數據集合之「中間(middle)」數值的唯一方法,我們還可以選擇計算中位數(median)。中位數本身更加切合作為一個數據集合之「中間」數值,因為它的計算方法是把集合中的數字由小至大排列出來,而位於正中間那個數字便是該集合的中位數。如果N是偶數的話,中位數便等於正中間那兩個數字之平均數,例如 {2, 5, 5, 8, 10, 12} 的中位數就是 (5+8) ÷ 2 = 6.5。
平均數與統計學中的一些重要概念如或然率(probability)和預期值(expected value)的關係,所以平均數最常被用來概括數據的特徵。可是平均數並非概括數據的永遠最好方法,其中一個中位數比平均數優勝的地方是前者不會受奇異值(outliers)(因某些異常情況而出現的極端數值,它對於所要研究的對象不具代表性)的不必要影響。譬如,由於一些不尋常的情況,數據 {2, 5, 5, 8, 10} 改變成 {2, 5, 5, 8, 100},對於這個數據之「中間」數值的結論,平均數會由6增加到24,但中位數就不受這個異常情況所影響而維持在5不變。
§3. 抽樣統計
很多時候,當有限的資源(例如人力、時間及財力等)令我們不能對研究對象(人、事或者物)的每一個分子進行資料搜集,我們便會採用抽樣統計(sampling)這個方法。一個抽樣統計要是準確和可靠,在它從樣本(sample)(總體的子集合)所搜集之數據所分析到的結果必須能夠推廣到總體(population)(整個研究對象的集合)上。然而,怎樣的抽樣統計才能達到這個目標呢?
首先,進行抽樣的時候要採用隨機抽樣法(random sampling)(或「或然率抽樣法(probability sampling)」),以確保總體之每一個分子都有相等被抽樣的或然率。相反,從非隨機抽樣法(nonrandom sampling)得來的樣本存有偏差(bias),即總體中的某些分子比其他的有較大機會被抽樣,因此所得的資料未必能夠推廣到總體本身。例如:假設天文台只在香港島裝置雨量器作為收集香港降雨量的資料,則這個抽樣方法就有偏差,因為香港島只是香港其中一個主要地域,所以香港島的降雨量(樣本)未能代表香港的降雨量(總體)。假若現在香港島、新界、九龍和大嶼山各區都裝置了雨量器以收集雨水,這樣的抽樣是否就免於偏差的問題呢?答案是否定的:若果雨量器所處的地方有些在野外空地、有些在樹蔭下、有些在瀑布或溪澗旁邊等等,那麼在某些地點落下的雨水被雨量器收集之或然率會比其它地點的高(位於某些地點的雨量器甚至連並非來自降雨的水也收集下來)。這個例子除了具體解釋「偏差樣本」的意思外,亦顯示了進行隨機抽樣時會有許多問題需要考慮。
但即使我們能夠用隨機抽樣法搜集到沒有偏差的樣本,這也未能代表所作之抽樣統計是準確和可靠的,因為所有從樣本所得的數據都會有抽樣誤差(sampling error)——樣本某方面的數據(例如平均數)偏離(因此不能代表)總體在同一方面的數據。[注1] 例如我們在某個荔枝園隨機而且毫無偏差地抽取了10顆荔枝去量度它們的平均直徑,可是這卻不能夠保證所抽取的並非園裡特別大或特別小的荔枝,那麼它們的平均直徑便不能代表該荔枝園中所有荔枝(總體)的平均直徑。假設我們抽取100顆荔枝做樣本,雖然同樣難保這100顆荔枝是園裡特別大或特別小的一類,但是今次發生這個情況的機會總應該比起只用10顆荔枝做樣本的時候為小。[注2] 由此我們知道,樣本數目(sample size)和抽樣誤差是成反比的。所以儘管任何抽樣都無法完全剔除抽樣誤差,但只要樣本數目之大能夠令抽樣誤差達到一個足夠低的水平,樣本的數據和總體的數據就應該不會有很大出入。但我們如何判斷抽樣誤差孰大孰小從而評價一個抽樣統計是否準確和可靠呢?
我們最常遇到、又是統計學中其中一個量度抽樣誤差的方法是信賴區間(confidence interval)。假設那100顆荔枝樣本的平均直徑和標準偏差(standard deviation)[注3]分別是25.4毫米和6.6毫米。首先計算出標準誤差(standard error)以估計樣本的平均直徑會偏離總體的平均直徑多少,方法是把標準偏差除以√n:6.6 ÷ √100 = 0.66。如果樣本數目是足夠大(例如大過30),則95%的信賴區間相等於樣本平均數加或減兩個標準誤差:25.4 ± (0.66 × 2) = 25.4 ± 1.32毫米[注4]。「25.4 ± 1.32毫米」這個95%的信賴區間的意思是倘若我們重複抽取100顆荔枝去量度它們之平均直徑,則在95%(5%)的時間裡面荔枝總體之平均直徑會(不會)在25.4 ± 1.32毫米這個數值範圍內。[注5]
最後,我們要清楚樣本誤差與樣本偏差之分別:樣本誤差純粹受樣本數目的影響(而且是反比關係),通常用信賴區間作為量度的標準(而信賴區間本身預設了所抽取之樣本沒有任何偏差);樣本偏差則受抽取樣本的方法或手段所影響,對它並沒有普遍的量度標準,須按不同的抽樣統計和研究對象個別考慮以作出評估,此外亦沒有一個普遍、簡單和直接的方法去減低樣本偏差。簡言之,樣本誤差與樣本偏差之間是不相關的(uncorrelated)。
§4. 相關性與因果關係
如果一件事情發生(不發生)會增加另一件事情發生(不發生)的機會,這兩件事情便是正相關的(positively correlated)(例如失業率和犯罪率);相反,如果一件事情發生(不發生)會減低另一件事情發生(不發生)的機會,這兩件事情是負相關的(negatively correlated)(例如空氣的相對濕度和山火);最後,假若一件事情發生(不發生)不會增加或者減低另一件事情發生(不發生)的機會,那麼這兩件事情便是不相關的(uncorrelated)或獨立的(independent)(例如體重和智商)。[注6]
有些事件例如失業率和犯罪率我們除了知道它們有相關性之外,我們亦知道失業率上升也是犯罪率上升的原因。但是我們不可以對凡具相關性的事件都作出同類型的推論——因為事件A和事件B有相關性,所以A是B的原因——否則我們便犯了居前為因的謬誤 (post hoc fallacy),原因是我們還未排除其它不同的解釋。
注
- 抽樣誤差本質上並非錯誤(mistake),因為只有對總體的每一個分子都進行調查(然而這就不是抽樣統計)才會得到與總體完全相等的數據,所以再完善的抽樣統計程序和方法都無法避免存有抽樣誤差(除非剛巧每一個樣本都具有和總體相同的特徵,那另當別論)。
- 可以想像極端的情況去理解這個直覺判斷:
假設該荔枝園總共有10000顆荔枝。樣本甲只抽取1顆荔枝,樣本乙則抽取9999顆荔枝,哪一個樣本的平均直徑會較接近園裡所有荔枝的平均直徑呢? - 標準偏差的計算方法是:
步驟一、(每個樣本數據 - 樣本全部數據之平均值)2。
步驟二、把步驟一所得的各個數值相加。
步驟三、把步驟二的結果除以 (n - 1)(「n」指樣本數目)。
步驟四、從步驟三所得的數值之平方根就是抽樣的標準偏差。 - 可見95%的信賴區間之闊度與 1/√n 成正比。假設想將抽樣誤差減半,那麼樣本數目便要增加到4n。
- 信賴區間很多時又叫做「誤差幅度(margin of error)」,譬如某選舉候選人支持率統計調查3%的誤差幅度,如果該調查的結果是選民對候選人甲之支持率為52%,則95%的信賴區間等於52 ± 3%。
- 這三種相關性可用或然率的公式分別表達如下:
- 事件A和事件B是正相關的,如果——P(A假如B) > P(A假如非B) 或 P(A假如B) > P(A)
- 事件A和事件B是負相關的,如果——P(A假如B) < P(A假如非B) 或 P(A假如B) < P(A)
- 事件A和事件B是不相關的,如果——P(A假如B) = P(A假如非B) 或 P(A假如B) = P(A)