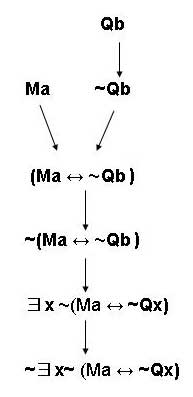[PL05] Well-formed formula

Module: Predicate logic

Quote of the page

Creativity takes courage.

- Henri Matisse

Popular pages

§1. Defintion

In these tutorials we will work with a simpler version of predicate logic (using only one-place predicate letters). We will call this monadic predicate logic, or MPL. Let us first define the language of MPL more precisely:

The language of MPL contains the following symbols:

Predicate letters : A, B, C, ... Z. If a subscript is added to a predicate letter, the result is a predicate letter, e.g. A₁ , B₂₇₄, etc.
Names : a, b, c, ... t. If a subscript is added to a name, the result is a name, e.g. a₁, b₃₄, etc.
Variables : u, v, w, x, y, z. If a subscript is added to a variable, the result is a variable, e.g. x₁₁, y₃₂₃₃, etc.
Five sentential connectives :
- ~ (tilde, or the negation sign)
- & (ampersand, or the conjunction sign)
- ∨ (the wedge, or the disjunction sign)
- → (the arrow)
- ↔ (the double-arrow)
- Open and close brackets : ( )
The two quantifiers: ∃, ∀.

An expression of MPL is a string of one or more symbols of MPL.

The syntactic rules, or formation rules (rules of formation), for MPL are as follows :

Any predicate letter, or any predicate letter followed by a name, is a wff.
Any predicate letter not followed by a name or a variable is a sentence letter.
If φ is a wff, then ~φ is a wff.
(φ&ψ), (φvψ), (φ→ψ), (φ↔ψ) are also wffs, if (a) φ and ψ are wffs, and (b) if any predicate letter ω appears in both φ and ψ, then either all occurrences of ω are sentence letters, or none of them are.
If φ is a wff that contains any name ω, and β is a variable which does not occur in φ, then the resulting expression that is obtained by replacing one or more occurrences of ω with β and then attaching "∃β" or "∀β" to the front, is also a wff.
Nothing else is a wff.

Rule #1 tells us that expressions such as "R", "Pa", "Qb", "Gc" are wffs.

Rule #2 tells us that expressions such as "R", "P", "Q" are sentence letters, and "Pa", "Qb", "Gx" are not.

Rules #3 and #4 are just like rules from SL. We can apply them to form new wffs such as "~~Pa", "~((Pa&Sc)↔(~Q∨Ka))".

Part (b) of rule #4 is meant to rule out cases such as "(Pa&P)" as wff. Reason: This expression is formed from "Pa" and "P". They include the same predicate letter "P". But the first occurrence of "P" is not a sentence letter even though the second one is. So according to 4(b) they cannot be combined to form a wff. But the rule allows "(Pa&Pb)" to be a wff. "(P&P)" is also a wff.

Rule #5 is a little complicated. It applies only to wffs that include at least one name. So it applies to expressions such as "Qa", "(~Pa→Qb)", "(Pa&Qa)", but not "∃xFx". The rule says that we can pick a name in a wff, replace one or more occurrences of that name by a single variable, and then add either an existential or universal quantifier to the front. Here are some examples:

From "Qa", we can generate wffs such as "∃xQx", "∀yQy".
From "(~Pa→Sa)", we get "∃y(~Py→Sy)" or "∃x(~Px→Sx)" or "∃x(~Px→Sa)" or "∃x(~Pa→Sx)", or "∀x(~Px→Sx), or "∀y(~Py→Sa)" etc.
From "(~Qa→Qb)", we get "∃x(~Qx→Qb)", "∀z(~Qa→Qz)" (But not "∃x(~Qx→Qx)"!)
From "(Pa&Qa)", we can get "∃x(Px&Qa)" and then "∃y∃x(Px&Qy)" by applying rule #5 twice.

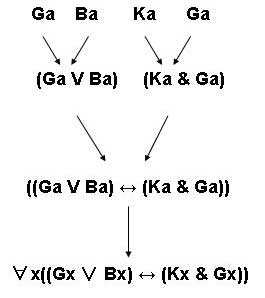
§2. Construction trees

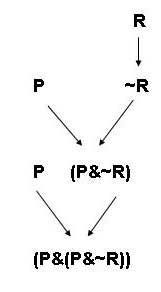
A complex wff in MPL is any wff that contains a quantifier or a connective. To show how a complex wff is constructed, we can draw a construction tree for that wff. A construction tree is a tree diagram with arrows linking wffs. Starting with non-complex wffs at the top, the diagram shows how a complex wff can be built up step-by-step using the formation rules of MPL. Here for example is a construction tree for "~(P&~Fa)" :

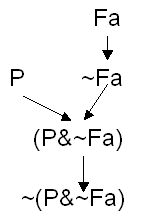
We started off with "P" and "Fa" which are not non-complex wffs. An arrow from X to Y indicates that Y can be constructed from X by applying one of the formation rules. Similarly, an arrow from X and Y to Z indicates that Z can be constructed from X and Y. By drawing a construction tree for a wff we show clearly how the formation rules are used to build up the wff. As a second example here is a construction tree for "~∀x(P&~Fx)" :

Of course, in this second example, we could have started off with "Fb" instead. So sometimes (not always) a wff can have more than one construction tree.

If any of these expressions is a WFF of MPL, draw its construction tree:

(P&(P&~R))
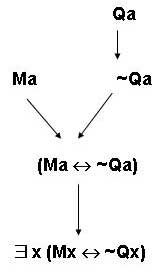
∃x(Mx↔~Qx)
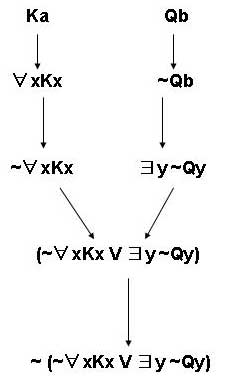
~(~∀xKx∨∃y~Qy)
~∃x~(Ma↔~Qx)
∃x(P→Qa)
Not a wff!
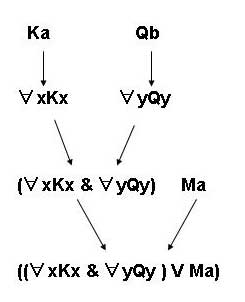
((∀xKx&∀yQy)∨Ma)
(∀xKx&((∀yQy)∨Ma))
Not a wff!
(∀yKx&∀xQy)
Not a wff!
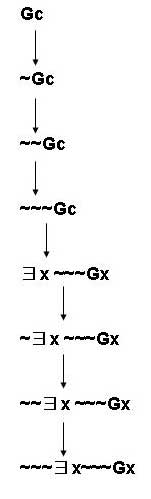
~~~∃x~~~Gx
(~∃x~Gx&Hy)
Not a wff!
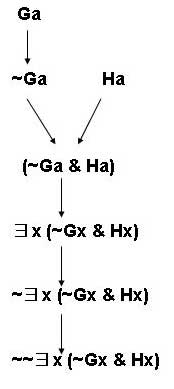
~~∃x(~Gx&Hx)
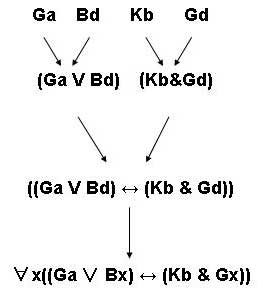
∀x((Ga∨Bx)↔(Kb&Gx))
∀x((Gx∨Bx)↔(Kx&Gx))

Do wffs in MPL have unique construction trees? In other words, given any wff in MPL, is it true that there is only one single construction tree that can be drawn for the wff? Why or why not?

previous tutorial next tutorial