[H28] 基本范氏圖
圖表法常常有助我們清楚地表示資訊。范氏圖解法便是一明顯例子。透過此方法,我們可清楚表達集合的性質及其間之關系,從而判斷某些論証的對確性。范氏圖以其創建人范恩命名。范恩曾任劍橋大學教授。在邏輯學及機率論上有不少建樹。本導修課將簡介范氏圖解法的基本概念及其基本應用。
§1. 集合
范氏圖可讓我們清楚表示集合或類的性質。簡單來說,一個集合或一個類就是一組事物。這些事物稱作該集合的份子或成員。例如,狗這個集合的成員就是所有個別的狗。
集合可被區分為有限集及無限集。所謂有限集,即只包含有限數目事物為其成員的集合。我桌上文具構成的集合,浸會大學1997年畢業生集合,以及SARS受害者集合均為有限集。無限集即包含無限數目事物為其成員的集合。自然數集,偶數集,及中文語句集皆屬無限集。
空集即沒有任何份子的集合。世上並無豬頭人身獸, 九腳狗, 漂亮的醜女,故而豬頭人身獸集, 九腳狗集, 漂亮的醜女集皆全為空集。
介紹過集合的概念後,現在讓我們看看如何以范氏圖標示集合的性質。范氏圖具有四個基本符號:
- 方塊
- 圓圈
- 陰影
- 剔號
§2. 方塊,圓圈,與區域
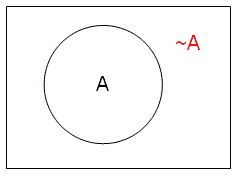
方塊與圓圈的作用在標示出區域。 每個區域代表某個由特定事物或個體構成的集合 。 方塊內的區域 (見下圖) 代表包含宇宙間一切事物的集合。你,我,我桌上的電腦,等等等等皆屬這個集合的成員。

在方塊內畫一個圓圈,我們便可標示出兩個不同的區域 。這兩個區域代表兩個不同的集合。假設圈內的區域代表人集(稱此集合為 'A'), 圈外的區域則代表非人集(稱此集合為 '~A')。世上所有人皆為A的成員,人以外的一切事物則屬 ~A的成員(見下圖)。
現在讓我們考慮包含一個圓圈以上的圖。先考慮包含兩個相交的圓圈。左邊的圓圈代表A集合,右邊的圓圈代表B集合。圖1清楚地標示出4個不同的區域:
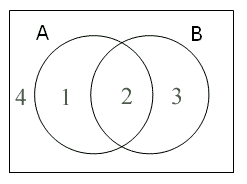
讓我們看看各區域分別代表什麼集合:
- 區域1 (以’A~B ’表示 ) 代表A與~B的交集:屬於這個集合的個體必需既為A又為非B。
- 區域2 (以’AB ’表示 ) 代表A與B的交集:屬於這個集合的個體必需既為A又為B。
- 區域3 (以’~AB ’表示 ) 代表~A與B的交集:屬於這個集合的個體必需既為非A又 為B。
- 區域4 (以’~A~B ’表示 ) 代表~A與~B的交集:屬於這個集合的個體必需既為非A又為非B。
假設A及B分別代表人集及男性集,那麼區域1至 4分別代表女人集 (歸屬於這區域的事物必需既為人又為非男性),男人集(歸屬於這區域的事物必需既為人又為男性),非人類的男性集(歸屬於這區域的事物必需既為人又為非男性),及非人類及非男性集合(歸屬於這區域的事物必需既非為人又為非男性)。
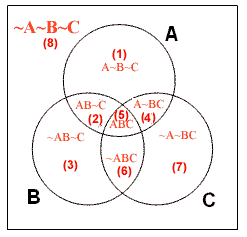
現考慮包含三個重疊相交的圓圈。我們看到下圖共分為八個區域,分別代表八個不同的集合 (A~B~C (1),AB~C (2),~AB~C (3),A~BC (4),ABC (5),~ABC (6),~A~BC (7),及~A~B~C (8))。
§3. 陰影與空集
現在讓我們看看如何符示集合的性質。在圓圈的某個範圍塗陰影表示該範圍所代表的集合為空集。假設我們想表示集合~AB為空集, 我們將如下符示:
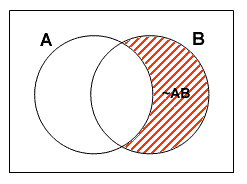
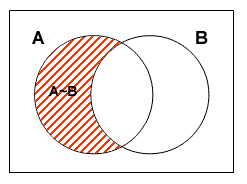
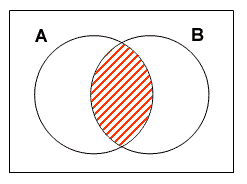
依同樣道理, 圖一及圖二中的陰影部份分別代表A~B及A B為空集。
圖一
圖二
§4. 剔號
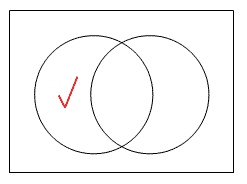
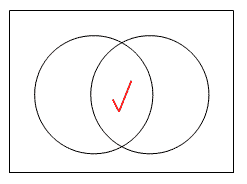
在某區域畫剔號代表該區域所代表的集合為非空集。換句話說,該區域所代表的集合至少有一個成員。例如,若要表示~AB有份子,我們可如下圖表示:
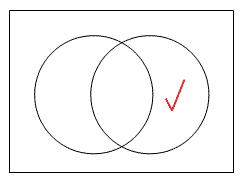
依同樣道理, 圖三及圖四中的剔號分別代表A~B及A B為非空集:
圖三
圖四
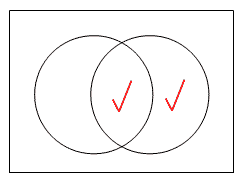
若要表示AB 及~AB區域分別代表的集合也為非空集,我們只需同時在兩個區域畫剔號,如下圖:
要避免從范氏圖讀取錯誤通訊,我們必須緊記以下兩點:
- 在某區域內有剔號只顯示該區域所代表的集合至少有一個份子;這並未顯示該集合共計有多少份子。有可能只有一個,也有可能有成千上萬個。
-
某區域沒有剔號並不意味該區域所代表的集合為空集。空區域傳達的唯一訊息是我們對該區域所代表的集合的份子數目並沒有任何知識。