[H29] 三段論與范氏圖
在後面章節我們將會看到,范氏圖的應用範圍並不太廣泛,許多論証的對確性也不能以此圖解法判定。然而,范氏圖卻提供我們一種簡易便捷的方法去判定三段論的對確性。現讓我們先看看何謂三段論。
§1. 三段論
每個三段論由兩個前提及一個結論組成。前提及結論皆為定言述句。我們可將定言述句粗略徵定為談及集合或類之間的關係的陳述。例如,「所有男人皆好學。」就為一定言述句。這述句共提及兩個類: 男人類及好學者類 (表示類的字詞一般被稱作「謂詞」。),並斷說任何事物,若屬男人類的成員,則也屬好學者類的成員。「有些科學家是哲學家。」也屬定言述句。這陳述談及兩個不同的類,且述說世上至少有一個個體是科學家類及哲學家類的成員。
傳統上,定言述句被區分為四種類形, 並分別以A,E,I,及O命名:(1) 全稱肯定句: 具「所有X都是Y。」形式的述句 (例,「所有人都有肺。」,「所有女人都有丈夫。」) ;(2) 全稱否定句:具「沒有X是Y。」(或「所有X都不是Y。」) 形式的述句 (例,「沒有大學生是愛讀書的。」,「所有國王都不是禿頭的。」);(3) 特稱肯定句:具「有些X是Y。」形式的述句 (例,「有些鳥是會飛的。」,「有些書是值得讀的。」) ; (4): 特稱否定句:具「有些X不是Y。」形式的述句 (例,「有些人不懂得自愛。」,「有些哲學家不懂得科學。」)。
「所有」,「一切」,「每個」,「沒有」,及「有些」等詞因用以顯示數量,故被稱作「量詞」。為修辭之美,許多時候定言述句會省略「所有」,「有些」等量詞 (讓我們稱這些述句為「非標准式定言述句」。) 。 很明顯,「人死不能復生。」,「人不為己,天誅地滅。」, 「男兒志在四方。」等皆為定言述句, 雖然有時我們對這些述句屬全稱述句還是特稱述句可能並不太清楚。
每個三段論包含三個謂詞。此外,每個謂詞均重覆兩次 (然而,不能在同一述句重覆兩次。)。
現舉一些三段論的具體例子:
例一:
1. 所有小孩子皆愛吃糖。
2. 所有愛吃糖者皆有蛀牙。
3. 所有小孩子皆有蛀牙。
例二:
1. 所有哲學家都是聰明的。
2. 有些科學家是聰明的。
3. 有些科學家是哲學家。
例三:
1.任何大學生都曾經逃學。
2.有些大學生是厭惡文學的人。
3.有些厭惡文學的人曾經逃學。
例四
1.一切有為法,如夢幻泡影。
2.任何如夢幻泡影之物皆不值得追求。
3.有些有為法並不值得追求。
綜上所述,任何論証為三段論當且僅當滿足以下所有條件:
- 具有兩個前提及一個結論。
- 前提及結論皆為定言述句。
- 前提及結論包含三個謂詞並提及三個集合。
- 試從日常言談中找出五句非標准式定言述句。
- 試舉出五個三段論,並指出這些論証的前提及結論屬定言述句的何種 形式。
§2. 范氏圖解法的基本步驟
介紹過三段論後,現在我們看看如何以范氏圖品評三段論。品評論証好壞通常需涉及許多不同層面。與大部份的邏輯技巧一樣,范氏圖解法只關注論証對確性的層面。
對確性這概念可以許多不同方式闡明。以下兩種為最常見之方式 (雖然也許並非最精確):
- 一個論証為對確的當且僅當若該論証前提全真,其結論也必為真。換句話說,不可能前提全真而結論假。
- 一個論証為對確的當且僅當該論証的結論訊息內容已被其前提的訊息內容所包含。故而,若某論証的結論之訊息超於其前提,該論証則一定不對確。
未開始詳述講解范氏圖解法前,讓我們先簡要陳述此方法之基本步驟:
- 畫三個圓圈以代表論証提及的三個不同集合。
- 以陰影或剔號表示前提所表達的資訊。
- 從畫好的圖中讀取資訊,從而判斷結論的資訊是否已被前提所包含。若答案為是,論証為對確。若為否,論証則不對確。
§3. 應用范氏圖解法
現在讓我們以例一至四說明范氏圖解法。
例一
步驟一: 畫三個相互交疊的圓圈代表例一提及的三個集合(以‘A’代表男人集,‘B’代表好學者集,及以‘C’代表早死的東西集。) 。如下圖:
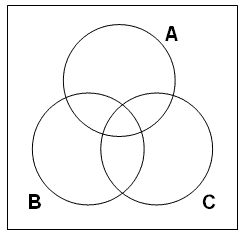
步驟二:畫好圓圈後,我們須考慮如何表示前提一及二所表達的資訊。在例一中,前提一述說沒有既是男人又不好學的個體。換言之,男人集及好學者集的交集是空集。因此,我們應在代表A~B~C及A~BC的區域塗上陰影。前提二述說沒有個體既好學但又不早死。因此,我們需在代表AB~C及~AB~C塗上陰影 (緊記: 某一區域沒有塗陰影只意味我們對該區域代表的集合無任何資訊,並不意味該區域所代表的集合並非空集。)。如下:
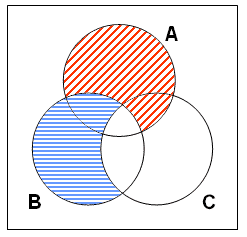
步驟三: 畫好圖後,我們要從圖中讀取資訊以判斷論証是否對確 — 結論的資訊是否已被前提所包含。若答案為是,論証為對確。若答案為否,論証則不對確。例一的結論述說男人及非早死者的交集為空集。以圖表示,則應把代表A~B~C及AB~C的區域塗上陰影。在上圖我們可以清楚看到,此區域已有陰影。這表明結論之訊息內容已被前提所包含。故此,我們得知,例一為對確的三段論。
例二
步驟一: 先畫三個相交的圓圈以代表代表例二提及的三個集合(以‘A’代表哲學家集,’B’代表聰明的東西集,‘C’代表科學家集),如下圖:

步驟二: 前提一述說不聰明的哲學家是不存在的 (不聰明的哲學家這集合是空集)。故應在代表A~B~C及A~BC的區域填陰影。如下圖:
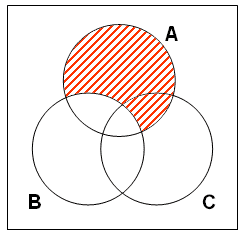
前提二說至少有一個聰明的科學家。只要滿足以下任何一種情況,前提二都為真:
- ABC有份子。
- ~ABC有份子。
- ABC及~ABC皆有份子。
然而,從前提二,我們並無從確切得知這三種情況何者為真。為表示這處境,我們將在代表ABC及~ABC之區域之交界畫上剔號。見下圖:
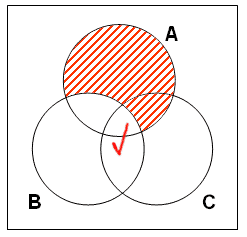
步驟三: 結論述說科學家與哲學家的交集有份子。因此,若此結論的訊息已被前提所包含。我們應該在代表ABC的區域內發現剔號。然而,圖中只顯示代表A~BC的區域被填上陰影及在代表ABC及~ABC之區域之交界處有剔號。因此,我們得知,例二並非對確。
例三
步驟一: 畫三個圓圈以代表例三提及的三個集合 ('A' 代表大學生集,'B' 代表愛逃學的人集,'C' 代表厭惡文學的人集),如下圖:

步驟二: 前提一說沒有大學生不愛逃學 (大學生集與不愛逃學的人集之交集為空集)。故我們該分別在代表A~B~C及A~BC之區域填陰影。前提二說至少有一個大學生厭惡文學。因此在代表A~BC及ABC之區域間之交界應記下剔號。然而由於代表A~BC之區域已被填陰影, 故我們只需在代表ABC之區域加上剔號,如下圖:
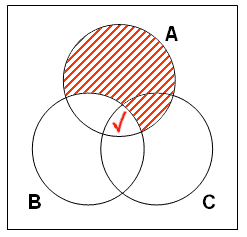
步驟三: 結論說至少有一個大學生是厭惡文學的人 (大學生集與厭惡文學的人集的聯集有份子)。因此,只要我們在代表ABC或~ABC之區域發現剔號,結論便為真。在上圖清楚顯示,代表ABC之區域已有剔號。這表示前提已包含結論的訊息。因此,例三為對確。
例四
步驟一:畫三個圓圈以代表例四提及的三個集合 (A代表有為法集, B代表如夢幻泡影之物集,C代表值 追求之物集)。看下圖:

步驟二: 前提一說有為法集與非如夢幻泡影之物集之交集為空集。故我們須在代表A~B~C及A~BC之區域填陰影。前提二說沒有如夢幻泡影之物的東西是值追求之物,故ABC及~ABC也需填陰影。如下圖:

步驟三: 結論說有些有為法是不值追求之物。因此,只要我們在代表A~B~C或AB~C之區域發現剔號,結論便為真。然而,上圖卻沒如此顯示。由此,我們可得知,結論的內容沒被前提所包含。因此,例四不對確。