[T09] Sampling error
Module: Basic statistics
- T00. Introduction
- T01. Basic concepts
- T02. The rules of probability
- T03. The game show puzzle
- T04. Expected values
- T05. Probability and utility
- T06. Cooperation
- T07. Summarizing data
- T08. Samples and biases
- T09. Sampling error
- T10. Hypothesis testing
- T11. Correlation
- T12. Simpson's paradox
- T13. The post hoc fallacy
- T14. Controlled trials
- T15. Bayesian confirmation
Quote of the page
The heart of man is made to reconcile the most glaring contradictions.
- David Hume
Help us promote
critical thinking!
Popular pages
- What is critical thinking?
- What is logic?
- Hardest logic puzzle ever
- Free miniguide
- What is an argument?
- Knights and knaves puzzles
- Logic puzzles
- What is a good argument?
- Improving critical thinking
- Analogical arguments
Suppose we succeed in obtaining a truly random sample of fish from a given area of sea, and we calculate the mean mercury level in our sample. Will this level tell us the mean mercury level in local fish overall? Not necessarily. Suppose our random sample consists of two fish. What guarantee do we have that the mercury level in these two fish is representative of the mercury level in the population overall? It could well be that both of these fish just happen to have particularly high levels, or particularly low levels.
What if we take a sample of a hundred fish? Again, it's possible that all these fish have particularly high or particularly low mercury levels, in which case our sample mean doesn't accurately represent the population mean. But intuitively, this seems much less likely in the case of a hundred fish than in the case of two fish. If the fish are really chosen at random, it seems like we would have to be very unlucky to get a sample of fish which had a very different mean mercury level than the population at large.
In fact, this intuition can be given a rigorous statistical justification. The basic idea is that for a small sample, any quantity you calculate has a large sampling error. The sampling error provides a measure of how likely it is that the quantity you have calculated is a specified distance from the true population value. The larger the sample, the smaller the sampling error. Note that sampling error isn't an error in the sense of a mistake; every figure calculated from a sample has a sampling error, however good the sampling process. Due to the chance nature of random sampling, you can never completely eliminate the possibility that your sample is misleading. But if the sampling error is small enough, that tells you that it is unlikely that your calculated value is a long way from the true value in the population.
Several different statistics can be used as a measure of the
sampling error, but the one you will encounter most frequently
is called a confidence interval. For example, suppose
you collect a random sample of 100 fish, measure their mercury
levels, and calculate the mean and standard deviation of the
results. Suppose you obtain a mean of 0.265 ppm (parts per
million) and a standard deviation of 0.081 ppm. Your best
estimate of the mean mercury level of the fish in the
population as a whole is 0.265 ppm, but how far is this likely
to be from the true population mean? Using the standard
deviation of the sample, you can calculate a quantity called
the standard error by dividing the standard deviation
by
![]() , where n is the sample size. In our case, then
the standard error is given by 0.081/10 = 0.0081. As long as
the sample is reasonably large (say, more than 30), the 95%
confidence interval is an interval of two standard errors on
either side of the sample mean. In our case, then, the 95%
confidence interval for the mean mercury level in local fish
is 0.265
±
0.016 ppm.
, where n is the sample size. In our case, then
the standard error is given by 0.081/10 = 0.0081. As long as
the sample is reasonably large (say, more than 30), the 95%
confidence interval is an interval of two standard errors on
either side of the sample mean. In our case, then, the 95%
confidence interval for the mean mercury level in local fish
is 0.265
±
0.016 ppm.
What does the 95% confidence interval tell us? Often, statistics books say things like the following: We can have 95% confidence that the true population mean lies between 0.249 ppm and 0.281 ppm. But this is slightly misleading, as it suggests that confidence intervals are about a particular kind of feeling of confidence you should have towards your result. What the confidence interval actually means is that if you take random samples of 100 fish over and over again, then 95% of the time, the confidence interval will contain the true population mean. Only 5% of the time will the true population mean lie outside the confidence interval, so you would have to be quite unlucky for the confidence interval not to contain the true mean. How this is connected with any feeling of confidence you may have about your result is a difficult philosophical question.
Note that the width of the 95% confidence interval is
proportional to 1/
![]() , where n is the sample size. In
fact, this is generally true of all measures of sampling
error. This provides a useful link between sampling error and
sample size; for example, if you want to cut your sampling
error in half, you need to multiply the size of your sample by
four. Sampling error is purely a result of the size
of the sample, unlike bias, which is a result of the way the sample is collected.
, where n is the sample size. In
fact, this is generally true of all measures of sampling
error. This provides a useful link between sampling error and
sample size; for example, if you want to cut your sampling
error in half, you need to multiply the size of your sample by
four. Sampling error is purely a result of the size
of the sample, unlike bias, which is a result of the way the sample is collected.
Confidence intervals are often found in reports of the results of surveys and political polls. For example, political polls often quote a "margin of error", usually of around 3 percentage points. What this means is that the 95% confidence interval is the cited figure plus or minus 3 percentage points. If the poll says that 52% of voters support Lee, then the 95% confidence interval is 52 ± 3%. In 95% of such polls, you can expect the true level of voter support to be within the confidence interval. Remember, though, that the confidence interval is just a measure of the sampling error; it assumes that the sampling method has ruled out all sources of bias, which as we have seen, is very difficult to achieve.
Suppose that Lee hires a pollster to estimate his support in the forthcoming election. A poll of 1000 people indicates that he has the support of 52% of people, with a margin of error of 3 percentage points. Lee would like a more accurate estimate. How many people would need to be polled in order to reduce the margin of error to 1 percentage point?
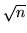 , where n
is the sample size. So to reduce the margin of error by a
factor of 3, we need to increase the sample size by a factor
of 9. (If n becomes 9 times bigger, the margin of error
becomes
, where n
is the sample size. So to reduce the margin of error by a
factor of 3, we need to increase the sample size by a factor
of 9. (If n becomes 9 times bigger, the margin of error
becomes
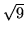 = 3 times smaller.) Hence to achieve a
margin of error of 1 percentage point, we would need to
increase the sample size from 1000 to 9000. This example shows why decreasing the sampling error beyond a certain point quickly becomes impractical. It is quite likely
that sampling 9000 people for a political poll would be
prohibitively expensive. Furthermore, there may be unavoidable
biases in the sampling techniques (as discussed in the
previous section), which introduce additional sources of error
in the estimate. Increasing the sample size does nothing to
reduce these errors.
= 3 times smaller.) Hence to achieve a
margin of error of 1 percentage point, we would need to
increase the sample size from 1000 to 9000. This example shows why decreasing the sampling error beyond a certain point quickly becomes impractical. It is quite likely
that sampling 9000 people for a political poll would be
prohibitively expensive. Furthermore, there may be unavoidable
biases in the sampling techniques (as discussed in the
previous section), which introduce additional sources of error
in the estimate. Increasing the sample size does nothing to
reduce these errors.