[T02] The rules of probability

Module: Basic statistics

Quote of the page

I must be allowed to add some explanatory remarks to bring the subject home to reason—to that sluggish reason, which supinely takes opinions on trust, and obstinately supports them to spare itself the labour of thinking.

- Mary Wollstonecraft

Help us promote
critical thinking!

Popular pages

For reference, here is a list of the rules of probability:

Addition rule:

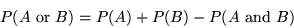
$\begin{displaymath}P(A \mbox{ or } B) = P(A) + P(B) - P(A \mbox{ and } B) \end{displaymath}$
Special addition rule (for mutually exclusive events):

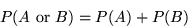
$\begin{displaymath}P(A \mbox{ or } B) = P(A) + P(B) \end{displaymath}$
Subtraction rule:

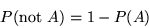
$\begin{displaymath}P(\mbox{not } A) = 1 - P(A) \end{displaymath}$
Multiplication rule:

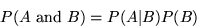
$\begin{displaymath}P(A \mbox{ and } B) = P(A\vert B)P(B) \end{displaymath}$
Special multiplication rule (for independent events):

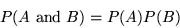
$\begin{displaymath}P(A \mbox{ and } B) = P(A)P(B) \end{displaymath}$

It is important to bear in mind the circumstances in which the special addition rule and the special multiplication rule can be used. Most mistakes in probabilistic reasoning occur because someone assumes that events are independent when they are not (or vice versa), or because someone assumes that events are mutually exclusive when they are not (or vice versa).

Here is the original problem which led Pascal and Fermat to develop probability theory:

The gambler's problem

Suppose you roll a single die four times; what is the probability of rolling at least one 6? The gambler reasoned that since the chance of a 6 in each roll is 1/6, the chance of a 6 in 4 rolls is 4 x 1/6 = 2/3. Now suppose you roll a pair of dice 24 times; what is the probability of rolling at least one double 6? The gambler reasoned that since the chance of a double 6 in one roll is 1/36, the chance of a double 6 in 24 rolls is 24 x 1/36 = 2/3. In other words, the gambler expected to win each bet 2/3 of the time. His problem was that he seemed to lose more often with the second bet than the first. He was at a loss to explain this, so he asked his friend Pascal for an answer.

What are the mistakes in the gambler's reasoning? What are the true probabilities of winning each bet?

§1. Examples and fallacies

A fallacy is a mistake in reasoning. The following examples each contain some reasoning about probabilities, some of which is correct and some of which is mistaken. See if you can spot any mistake, and then click "correct" if you think the reasoning is o.k. and "fallacy" if you think it is wrong.

Fred is playing roulette in a Macau casino. The roulette wheel has 36 numbers (ignoring the zero), of which half are red and half are black. Fred reasons as follows: In the last ten spins, all the winning numbers have been red. But on average, only half the winning numbers are red. So to even things out, there must be more black numbers than red numbers coming up. So I stand a better chance of winning if I bet on black. or
Yes, the reasoning is fallacious. The outcomes of the previous ten spins of the wheel can have no effect on the motion of the wheel and the ball; past outcomes can't affect future outcomes. In other words, the outcomes are independent. The probability of a black number is still 1/2 on each spin, irrespective of what has come before. For obvious reasons, this kind of mistake is called the gambler's fallacy. It is a very common mistake.
?
The chance of the Mark Six numbers being exactly the same two days in a row is extremely small. So to maximize my chances of winning today, I should not choose yesterday's winning numbers.
No, this reasoning is fallacious. Go back and ask yourself: What is the chance of winning if I choose yesterday's numbers? What is the chance of winning if I don't choose yesterday's numbers?
or
Yes, the reasoning is fallacious. It is another instance of the gambler's fallacy, since the winning numbers today are entirely independent of the winning numbers yesterday. This version of the gambler's fallacy is very tempting, as it is true that the probability of the same numbers coming up two days in a row is very small--about one in 10 million. So the chance of winning if you pick yesterday's numbers is only one in 10 million. But notice that the chance of winning is the same whatever numbers you choose; for any set of six numbers you choose, the chance of getting them all correct is one in 10 million. In fact, an argument can be made that you are better off picking yesterday's numbers. That is because if two people win, they have to share the prize. Since people tend to avoid yesterday's numbers (as well as "unlucky" numbers like 13), if you choose yesterday's numbers you are less likely to have to share your prize!
?
Suppose I am at the Pokfield Road bus terminus, waiting for the number 23 bus to leave for North Point. The number 23 leaves from here every 8 minutes. So the longer I wait for the bus, the higher the probability that it will leave in the next minute.
Yes, this reasoning is correct. Superficially, this case resembles the prior two examples, but the difference here is that the chance of a bus coming in a given minute is not independent of what happened in the previous minutes, since the buses are timed to be a fixed number of minutes apart. When you first arrive at the bus stop, the bus has an equal chance of coming in each of the next 8 minutes, so the probability of it coming within one minute is 1/8. If it doesn't come in the first minute, then it must come in one of the following 7 minutes, so the probability of it coming within one minute goes up to 1/7. If it doesn't come in the first two minutes, the probability of it coming within one minute goes up to 1/6. And so on.
or ?
A city has a crackdown on speeding drivers, and the number of traffic fatalities falls by 12%. The local government claims that the increased enforcement has saved lives. But the crackdown was started because of a sudden increase in traffic fatalities the prior year. After an unusually high value, the number of deaths is likely to fall the following year anyway. So there is no reason to think that the crackdown caused the decrease in fatalities.
Yes, this reasoning is correct. In general, it is more probable that you will get a number of traffic fatalities that is close to average than one which is far higher than average. This is true whatever the number was for the prior year, since presumably the numbers of traffic fatalities in different years are largely independent. So for this year, it is likely that the number of traffic fatalities will be not too far from average, in which case it will be lower than last year's unusually high value. Statisticians call this phenomenon regression to the mean.
or
No, this reasoning is correct. This case is quite tricky. It looks at first glance like a version of the gambler's fallacy, since the number of traffic fatalities in one year is presumably independent of the number of fatalities the prior year. But in fact it is not a fallacy; the very fact that this year's fatalities are independent of last year's means that this year's rate is likely to be lower than last year's. It might help to think about the following analogy: Suppose you roll five dice, and you get four sixes (which is an unusually high number of sixes--you can calculate the probability). What is the chance of getting four or more sixes on the next roll? What is the chance of getting fewer than four sixes? Go back and think about how that applies to this case.
?
"BALTIMORE (AP) A Maryland woman this week gave birth to triplets for the second time in less than two years, defying odds of about one in 50 million, hospital officials said." The reasoning here is that since only about one birth in seven thousand is of triplets, the odds of having two sets of triplets in a row is about one in 7000², which is one in 50 million. or
Yes, this reasoning is almost certainly fallacious. The odds of one in 50 million were calculated using the simplified multiplication rule, which only applies if the two events are independent. But giving birth to triplets the second time may well not be independent of giving birth to triplets the first time; the woman may have a biological predisposition for multiple births. In that case, the probability of the second set of triplets--the probability of a woman giving birth to triplets given that she has already had triplets--may be considerably greater than 1/7000. The chance of having two sets of triplets is obtained by multiplying this probability by the chance of having the first set of triplets (1/7000). This chance is still very small, but it may be nowhere near as small as reported.
?

previous tutorial next tutorial