[SL] Sentential logic
In formal logic, we develop different systems of symbols and rules to express ideas and carry out proofs. There are lots of such formal systems. In this module we discuss Sentential Logic (SL). It is one of the simplest formal systems of logic, and is also known as "Propositional Logic".
Before you begin, p check that your browser can display the logic symbols used in this module. These are the symbols:
≡ ∨ ↔ → ∃ ∀ ψ φ α β ⊧
They should look like the ones in this picture:
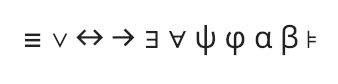
If not, try a more advanced browser, such as Chrome.
Tutorials
- [SL01] Introduction
- [SL02] Well-formed formula
- [SL03] Connectives
- [SL04] Complex truth-tables
- [SL05] Properties & relations
- [SL06] Formalization
- [SL07] Validity
- [SL08] The indirect method
- [SL09] Indirect method: exercises
- [SL10] Material conditional
- [SL11] Derivations
- [SL12] Derivation rules 1
- [SL13] Derivation rules 2
- [SL14] List of derivation rules
- [SL15] Derivation strategies
- [SL16] Soundness
- [SL17] Completeness
- [SL18] Limitations
What next?
After you have finished this module, try our next module on predicate logic!
Further readings
- A very good informal introduction: Graham Priest - Logic: A Very Short Introduction
- An introduction to formal logic. Used to be the standard textbook for first year logic students at Oxford: Wilfrid Hodges - Logic
- Harry Gensler - Introduction to Logic
- Does not presuppose any background but advances very quickly. Highly recommended if you are interested in the connections between computation, mathematics and logic. Written by the late George Boolos, a brilliant logician and philosopher at MIT: Computability and Logic
- Many advanced topics included: Theodore Sider - Logic for Philosophy
- A good formal logic textbook if you want to learn about more advanced topics related to Gödel's incompleteness proof and computability theory, by Richard E. Hodel: Introduction to Mathematical Logic
- Free online textbook on basic formal logic: http://tellerprimer.ucdavis.edu
- A good logic self-study guide (PDF): Teach Yourself Logic 2017: A Study Guide
- Entries on logic in the Stanford Encyclopedia of Philosophy - These are articles that discuss some of the main issues in the philosophy of logic. They are difficult!