[SL12] Derivation rules 1

In the previous tutorial you learned three rules. This section and the next describe the remainder of the rules of our system. There are 9 more rules, for a total of 12 rules in all.

If you are impatient, here is a list of all of the rules.

At this point, there won't be much discussion about why the rules are the way they are, or whether the rules should be the way they are. We'll get to that in Topic RS. For now, just work on learning what the rules are, and how the rules work.

§1. Rules for "&"

The conjunction elimination rule, &E was mentioned earlier. Let us state this rule carefully.

According to this rule, if one of the lines of a derivation is a conjunction, (φ&ψ), then you can add a new line which is φ or you can add a line which is ψ. The greek letters 'φ' and 'ψ' stand for any well-formed formula of sentential logic. Note that the dependencies of the new line are just the same as the dependencies of the original line. That is what the rule means when it says that the formula you write down depends on "on everything (φ&ψ) depends on."

&E helps you simplify things. You can eliminate the symbol '&' and write down only part of a formula. That is why &E is called an "elimination" rule.

But sometimes you might not want to eliminate '&', but to add it into a derivation. Sometimes you might want to write down a formula which contains an '&' when that '&' wasn't there before. There is a rule for that:

For most of the connectives, the rules in the system come in pairs like these rules for '&'. There is an elimination rule, and an introduction rule. The elimination rule lets you get rid of a symbol, and the introduction rule lets you add a symbol when the symbol was not there before.

Rule &I says that if one of the lines of a derivation is φ and one of the lines in the derivation is ψ then you can add a new line which is their conjunction: (φ&ψ). The dependencies of the new line are the same as all of the dependencies for the line with φ put together with all of the dependencies for the line with ψ. Here are two brief examples:

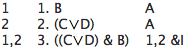
Is this a correct derivation?

answer

1  1. (A&B)	A
1  2. B 	1 &E
1  3. A 	1 &E
1  4. (B&A)	2,3 &I

§2. Rules for "↔"

The rules for '↔' are straightforward. Here is an example of a use of the biconditional elimination rule:

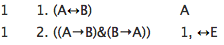
And, unsurprisingly then, here is the introduction rule:

Thus ↔E lets you change a biconditional into the conjunction of two conditionals. And ↔I lets you move in the opposite direction. The dependencies work just as they do for &E: the new dependencies are the same as the old dependencies. For both ↔E and ↔I, you just write down the same dependencies as before.

Stated explictly:

You have now seen half of the rules in the system: &I, &E, A, →E, ↔E, and ↔I. We will get to the rest of the rules in a moment. But first, you should try deriving a few things.

	1 	1. (A↔B) 		A
	2 	2. (B&C)		A
	2 	3. B 			2 &E
	1 	4. ((A→B)&(B→A))	1 ↔E
	1 	5. (B→A)      		4 &E
	1,2	6. A			3, 5 →E
	

	1 1. (A→A)		A
	1 2. ((A→A)&(A→A))	1, 1 &I
	1 3. (A↔A)		2 ↔I
	

	1 	1. (A↔B) 		A
	2	2. (B↔C)		A
	3 	3. A			A
	1	4. ((A→B)&(B→A))	1 ↔E
	1 	5. (A→B)		4 &E
	1,3	6. B			3, 5 →E
	2	7. ((B→C)&(C→B))	2 ↔E
	2	8. (B→C) 		7 &E
	1,2,3	9. C			6, 8 →E		
	

§3. Rules for "→" and the Rule of Assumption

Rule →E was introduced in section DS01:

Sometimes a rule like →E is called, using a Latin expression, Modus Ponens. But we'll just call it Conditional Elimination, or →E for short. An example of a use of such a rule in English would be:

If John has measles then Harry has measles.
John has measles.
Therefore, Harry has measles.

As this seems clearly to be an example of good reasoning, you can see why we might like to have a version of this rule in our logical system.

The introduction rule, →I, is a little different from the other rules you have seen. One important difference is that →I permits you to decrease the number of dependencies.

Consider this short example showing B ⊢ (A → (A&B)).

Notice that dependency of line 4 is only line 2, while line 3 has two dependencies: line 1 and line 2. Applying the rule →I yields the conditional on line 4 depending on everything line 3 depends on except line 1. Since line 3 depends on 1 and 2, line 4 depends on just 2. The idea behind →I is that if you can show ψ given an assumption φ, then you have shown that if φ then ψ, that is (φ→ψ). Here is the rule stated explicitly:

Rule →I provides a powerful, direct way to derive a conditional, (φ→ψ). You simply assume φ and then, using that assumption try to derive ψ. If you succeed, you will have thereby shown (φ→ψ). And this conclusion will no longer depend on the assumption φ. Assuming φ was just a temporary measure.

One point to keep in mind. Rule →I applies when you have assumed φ and derived ψ. Be careful: assuming and deriving are not the same. You have derived a formula when it is a line of the derivation you are working on. You have assumed a formula when it is written down in your derivation using the Rule of Assumption. The Rule of Assumption was explained in section DS01. Here it is again:

Is this a correct derivation?

answer

What is wrong with the following derivation?

answer

1	1. (P→(Q→R)) 		A
2	2. (P→Q)		A
3	3. P			A
2,3 	4. Q			2,3 →E
1,3 	5. (Q→R)		1,3 →E
1,2,3 	6. R			4,5 →E 
1,2	7. (P→R)		3,6 →I
1	8. ((P→Q)→(P→R))	2,7 →I

1 	1. A 		A
	2. (A→A) 	1,1 →I

1 	1. (A&B)	A
1 	2. A		1 &E
	3. ((A&B)→A)	1,2 →I