[SL15] Derivation strategies

The list of rules of our natural deduction system fits on one page. The rules are not very complicated, and there are not many rules.

Still, sometimes, it is not obvious how to make a certain derivation. And it is sometimes not obvious whether it is even possible to make a certain derivation.

How, for example, to show this?

~(P ∨ Q) ⊢ (~P & ~Q)

As a start, we might write:

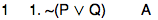
But now we are stuck. No obvious rule, like &E or →E, applies to line 1. Line 1 is not a conjunction, nor is line 1 a conditional. Line 1 is a negation.

What can we do?

In this section we will examine some strategies for making derivations.

§1. Do not make random assumptions

One rule that might apply to line 1 is ~E. If we can derive an explicit contradiction, then we can apply ~E to write down "(P ∨ Q)". To use ~E we need to find an explicit contradiction, but we only have line 1 so far. Now the Rule of Assumption lets us write down any formula we like.

So you might try this:

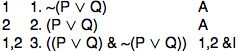
Now we have an explicit contradiction, and can apply Rule ~E:

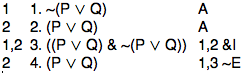
We have now shown (P ∨ Q) ⊢ (P ∨ Q).

That is no progress.

A mistake we just made was to think that if we need some formula, we should simply use the Rule of Assumption to assume it. This is a common beginner's mistake. Assumptions can be useful in making a derivation. But assuming things haphazardly is rarely an effective strategy in making a derivation.

We need a new approach.

§2. Think backwards

One approach is to try to see what rule to apply to line 1 in order to move a step closer to the conclusion. We just tried that. It didn't work.

Another approach is to think about things in the opposite direction: start with the last line and work backwards to the assumptions. Let's try that.

We know that the last line of the derivation should be "(~P & ~Q)" depending only on "~(P ∨ Q)":

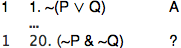
What rule could have been used on that last step? (Not knowing how many lines there will be when the derivation is finished, I just wrote "20" for the last line. I'll fix that later.)

Two possibilities are &I and ~E.

Are there any other rules that could have been used on the last line of that derivation? answer

Let's try &I.

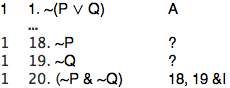
But now we seem to be stuck again. We need to show "~P" and "~Q". It is not obvious how to proceed.

§3. If you do not know what to do, try ~E or ~I

When you do not know what to do next, one of the negation rules is worth trying. In this case, since you want to show "~P", you can assume "P" and try to show an explicit contradiction.

If you succeed, you can write down "~P".

(I just guessed that the assumption will be on line 10. We can fix that later.) Now we are almost there. We just need to see how, somehow, to put "P" (on line 10) together with "~(P ∨ Q)" (on line 1) to get an explicit contradiction. One explicit contradiction is "(P & ~P)". However to get that we would need "~P", and "~P" is what we are using ~I to show. So that won't work. Another possibility is to get something which explicitly contradicts "~(P ∨ Q)" on line 1--- that is, to reach "(P ∨ Q)". And then we have the solution, once we realize that "(P ∨ Q)" follows from "P" in one step by rule ∨I:

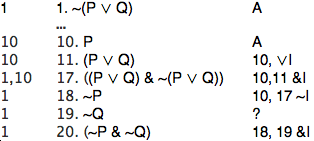
We have now succeeded in deriving "~P" from "~(P ∨ Q)".

That is, we have shown ~(P ∨ Q) ⊢ ~P.

This is what line 18 says.

However, we are not finished yet.

§4. Think about what you have proved before

We need to figure out how to reach "~Q" on line 19.

We need to show ~(P ∨ Q) ⊢ ~Q.

Sometimes in making a derivation, what you are trying to show is similar to something you have derived before. What we need to show now,

~(P ∨ Q) ⊢ ~Q,

is rather like what we have just shown,

~(P ∨ Q) ⊢ ~P.

Another useful strategy is to adapt a previous derivation to a new situation. In the previous derivation we used ~I, after assuming P. In this case, we can use ~I, after assuming Q:

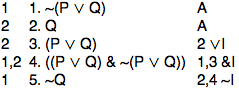
Now let's put the whole proof together, renumbering the lines appropriately.

Just take the derivation for ~(P∨Q) ⊢ (~P&~Q),
and substitute every occurrence of "P" with
"(A&B)"and "Q" with "C".

1	1. ~((A&B)∨C)			A
2	2. (A&B)			A
2  	3. ((A&B)∨C)			2 ∨I
1,2	4. (((A&B)∨C)&~((A&B)∨C))	1, 3 &I
1 	5. ~(A&B)			2, 4 ~I
6	6. C				A
6	7. ((A&B)∨C)			6 ∨I
1,6	8. (((A&B)∨C)&~((A&B)∨C))	1, 7 &I
1	9. ~C				6, 8 ~I
1	10. (~(A&B)&~C)			5, 9 &I

§5. Problem solving

By now you have seen several strategies for making derivations. Given the first few lines of the derivation, you can search for a rule which directly applies. It is also very useful to think backwards, looking for a rule which could have been used to get the last line. You can try to apply ~I or ~E. You can think about whether the derivation you are working on is like a derivation you have made already. And, as you have seen, in working out a derivation you can try all of these strategies.

But what you have not seen is a method that will work in every situation. There is no "model answer" to be memorized. Cases which appear similar may require very different methods. To improve your skills in solving problems, try the following further examples.

1	1. (P → Q)		A
2	2. (R → Q)		A
3 	3. (P ∨ R)		A
1,2,3 	4. (Q ∨ Q)		1,2,3 PC
5 	5. ~Q			A
1,2,3,5 6. Q			4,5 ∨E
1,2,3,5 7. (Q & ~Q)		5,6 &I
1,2,3 	8. Q			5,7 ~E
1,2	9. ((P ∨ R) → Q)	3,8 →I

1 	1. (A & B)	A
2 	2. (C & D)	A
1 	3. A		1 &E
2 	4. D		2 &E
1,2 	5.(A&D)		3,4 &I

1 	1. (P & (Q & R))	A
2 	2. S			A
1 	3. (Q & R)		1 &E
1 	4. R			3 &E
1,2	5. (R & S)		4,2 &I

1 	1. (P → Q)	A
2 	2. (Q → R)	A
3 	3. P		A
1,3 	4. Q		1,3 →E
1,2,3 	5. R		2,4 →E

1 	1. (P → (Q → R))	A
2 	2. (P & Q)		A
2 	3. P			2 &E
1,2 	4. (Q → R)		1,3 →E
2 	5. Q			2 &E
1,2 	6. R			4,5 →E

1	1. (P → (Q → R))	A
2	2. Q			A
3	3. P			A
1,3 	4. (Q → R)		1,3 →E
1,2,3	5. R			2,4 →E
1,2	6. (P → R)		3,5 →I

1	1. ((P & Q) → R)	A
2	2. P			A
3	3. Q			A
2,3 	4. (P & Q)		2,3 &I
1,2,3	5. R			1,4 →E
1,2 	6. (Q → R)		3,5 →I
1	7. (P → (Q → R))	2,6 →I

1	1. (P →(Q → R))		A
2 	2. (P → Q)		A
3	3. P			A
2,3	4. Q			2,3 →E
1,3	5. (Q → R)		1,3 →E
1,2,3	6. R			4,5 →E
1,2 	7. (P → R)		3,6 →I
1 	8. ((P→Q) → (P→R))	2,7 →I

1 	1. P 		A
2 	2. Q 		A
1 	3. (Q → P) 	2,1 →I

1	1. (P → Q)	A
2 	2. (Q → R)	A
3 	3. P		A
1,3	4. Q		1,3 →E
1,2,3	5. R		2,4 →E
1,2	6 (P → R)	3,5 →I

1 	1. ~(P & ~Q)		A
2	2. P			A
3	3. ~Q			A
2,3	4. (P & ~Q)		2,3 &I
1,2,3	5. ((P&~Q)&~(P&~Q)) 	1,4 &I
1,2	6. Q			3,5 ~E
1	7. (P → Q)		2,6 →I

1	1. P			A
2	2. ~P			A
3	3. Q			A
1,2	4. (P & ~P)		1,2 &I
1,2	5. ~Q			3,4 ~I

1	1. (~P → ~Q)		A
2	2. Q			A
3	3. ~P			A
1,3	4. ~Q			1,3 →E
1,2,3	5. (Q & ~Q)		2,4 &I
1,2	6. P			3,5 ~E
1	7. (Q → P)		2,6 →I

1	1. ((P ∨ Q) → R)	A
2	2. P			A
2	3. (P ∨ Q)		2 ∨I
1,2	4. R			1,3 →E
1	5. (P → R)		2,4 →I

1	1. ~(P → Q)		A
2	2. (~P ∨ Q)		A
3	3. P			A
4	4. ~P			A
3,4 	5. (P & ~P)		3,4 &I
3	6. ~~P			4,5 ~I
2,3	7. Q			2,6 ∨E
2	8. (P → Q)		3,7 →I
1,2 	9. ((P→Q) & ~(P→Q))	1,8 &I
1	10. ~(~P ∨ Q)		2,9 ~I

1	1. (P & (Q∨R))		A
1	2. P			1 &E
1	3. (Q ∨ R)		1 &E
4	4. Q			A
1,4	5. (P & Q)		2,4 &I
6 	6. R			A
1, 6	7. (P & R)		2,6 &I
1	8. (Q → (P & Q))	4,5 →I
1	9. (R → (P & R))	6,7 →I
1	10. ((P&Q)∨(P&R))	3,8,9 PC

1	1. (P ↔ ~Q)		A
2	2. (P ↔ Q)		A
2	3. ((P → Q) & (Q → P))	2 ↔E
2	4. (P → Q)		3 &E
1	5. ((P → ~Q) & (~Q→P))	1 ↔E
1	6. (P → ~Q)		5 &E
7	7. P			A
2,7	8. Q			4,7 →E
1,7	9. ~Q			6,7 →E
1,2,7	10. (Q & ~Q)		8,9 &I
1,2 	11. ~P			7,10 ~I
12	12. ~(Q ∨ ~Q)		A
13 	13. Q			A
13 	14. (Q ∨ ~Q)		13 ∨I
12,13	15. ((Q∨~Q) & ~(Q∨~Q))	12,14 &I
12 	16. ~Q			13,15 ~I
12 	17. (Q ∨~Q)		16 ∨I
12	18. ((Q ∨~Q)&~(Q ∨~Q))	12,17 &I
	19. (Q ∨~Q) 		12,18 ~E
2 	20. (Q → P)		3 →E
1 	21. (~Q → P) 		5 →E
1,2 	22. (P ∨ P)		19,20,21 PC
23 	23. ~P 			A
1,2,23 	24. P			22,23 ∨E
1,2,23 	25. (P&~P) 		23,24 &I
1,2 	26. P			23,25 ~E
1,2 	27. (P&~P)		11,26 &I
1 	28. ~(P ↔ Q)		2,27 ~I