[T06] Cooperation

Suppose you are working for an organization which opposes the government in an oppressive state, and you and one of your colleagues are arrested for distributing anti-government literature. You are taken to separate cells. The interrogator suspects you of being involved in a much larger plot to destabilize the government (which is true), but has no evidence, so he makes you the following offer. If you both say nothing, you will both be convicted of distributing anti-government literature, and will go to prison for one year. If you give evidence against your colleague, your colleague will be convicted of treason on the basis of your evidence, and will be executed, but you will go free. Conversely, if your colleague gives evidence against you, you will be executed for treason and your colleague will go free. Finally, if you both give evidence against each other, you will both be convicted of treason, but you will receive sentences of twenty years in prison in light of your cooperation. What should you do?

Suppose you assign a utility of -10 to death, -8 to twenty years in prison, -1 to a year in prison and 0 to going free, and suppose your colleague assigns the same utilities. Then we can represent the utilities of the various outcomes in the following table.

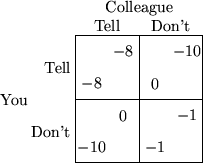
Your utilities are the numbers in the bottom left of each box, and your colleague's utilities are in the top right.

Of course, you don't know what your colleague is going to do. Suppose your colleague tells the interrogator what she knows. Then you get a utility of -10 if you don't tell, and -8 if you do, so you maximize your utility if you tell. On the other hand, suppose your colleague doesn't tell. Then you get a utility of -1 if you don't tell, and 0 if you do, so again you maximize your utility if you tell. So it doesn't matter what your colleague does; if you want to maximize your utility, you should tell.

Your colleague, though, if she also wants to maximize her utility, will reason in exactly the same way; whatever you do, she is better off telling. So if you both attempt to maximize your own expected utility, you will both tell, and both end up with a utility of -8 (twenty years in prison).

But something very strange has happened here. If you both keep quiet, you get only one year in prison--clearly a better outcome. By attempting to maximize your own utility, you each get a worse outcome than you would if you had both ignored your own utility! This puzzle is known as the prisoner's dilemma. It appears to be a case where individual self-interest prevents the best overall outcome from occurring.

The prisoner's dilemma is far more than just an idle philosophical example. It has attracted a good deal of attention from economists, political scientists, philosophers and even biologists. That's because it seems to have important consequences for general issues having to do with cooperation. For example, imagine a society with no law enforcement. In such a society, there is always a risk that your neighbor will break in when you are out and steal your possessions. If he does so, you would be better off if you went out and stole his things. In fact, even if he doesn't steal your things, you are still better off if you steal his things.

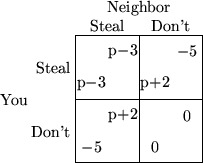
Again, we can use a table to represent the utilities of the various outcomes.

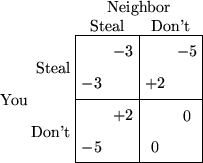
The worst outcome (-5) is having your things stolen without stealing anything back. If you steal some stuff back, the outcome isn't so bad (-3). If neither of you steals anything, the outcome is neutral (0), and if you steal things but nothing is stolen from you, you get an overall benefit (+2). Notice that the table has the same form as the prisoner's dilemma, and generates a similar conclusion. If you each act according to your own self-interest, you will both be constantly stealing each other's things (a utility of -3), whereas it would clearly be better if neither of you stole each other's things (a utility of 0).

An argument like this was first put forward by Thomas Hobbes. Hobbes used this argument as a justification for government; we need a government with the power to enforce laws so that it is no longer in the citizens' interest to attack each other (see the self-test question at the end of this section). The general point Hobbes tried to make is that cooperation is in the overall interest of the citizens of a country, but that self-interest alone is not always enough to produce cooperation.

Many political scientists think that such arguments still have relevance today, especially in the international arena. There is no "world government" capable of effectively enforcing cooperation between countries. The concern is that it may be in each country's self-interest to attack its neighboring countries, even though this may have disastrous overall consequences.

This kind of analysis of strategies of interaction is called game theory. The prisoner's dilemma is one of the "games" that are studied, but there are many more; a different structure of utilities gives a different game. For example, "free rider" problems can be studied using game theory. Whooping cough vaccinations provide an example of a free rider problem. The vaccine carries a small risk of serious side-effects. As long as most parents have their children vaccinated, then a few "free riders" can avoid the risk by not having their children vaccinated. However, if too many parents act this way, only a small proportion of children will be vaccinated, and there is a large risk of a serious epidemic.

Game theory originated in economics. However, it is now used in subjects as disparate as philosophy (e.g. to study the connections between self-interest and ethics) and biology (e.g. to study the mechanisms by which cooperative behavior in animals could evolve).

In the stealing example above, we assumed that there was no law enforcement. Now suppose that the government punishes people who steal. How big must the punishment be (in utility units) in order to deter self-interested people from stealing? If only 25% of thieves are caught, then how big must the punishment be?

answer

Suppose the punishment has utility p. Then the utility table becomes:

So if p has a utility value lower than -2, then it is in my interest not to steal, and similarly for my neighbor. If we both act in our own self-interest, given these punishments, we will each get a utility of 0.

If only 25% of thieves are caught, then the expected utility of punishment p is only p/4. So to deter stealing among self-interested people, the punishment must have a utility value lower than -8.