[V10] Limitations of Venn diagrams
Module: Venn diagrams
- V00. Introduction
- V01. Basic notation
- V02. Everything and nothing
- V03. Exercises
- V04. Three circles
- V05. Exercises
- V06. Existence 1
- V07. Existence 2
- V08. Syllogism
- V09. Exercises
- V10. Limitations of Venn diagrams
Quote of the page
I must be allowed to add some explanatory remarks to bring the subject home to reason—to that sluggish reason, which supinely takes opinions on trust, and obstinately supports them to spare itself the labour of thinking.
- Mary Wollstonecraft
Help us promote
critical thinking!
Popular pages
- What is critical thinking?
- What is logic?
- Hardest logic puzzle ever
- Free miniguide
- What is an argument?
- Knights and knaves puzzles
- Logic puzzles
- What is a good argument?
- Improving critical thinking
- Analogical arguments
Although Venn diagrams can help us reason about classes of objects, they also have many limitations. First of all, the diagrams can become too complicated to deal with if we are reasoning about many classes of objects. So far in our tutorials we have considered Venn diagrams with at most three circles. It is possible to add more bounded regions if we are dealing with more than three classes, but then the resulting diagrams will become rather difficult to handle and interpret. It is very easy to make mistakes when we encode information in such diagrams.
The other problem with Venn diagrams is that they have limited expressive power. What this means is that there are many pieces of information that cannot be accurately represented. For example, our system of notation allows us to talk about classes of objects, but not particular individual objects. For example, to say that a and b are cats and c and d are not, we might have to introduce new symbols, using dots to represent individuals, as in the diagram below:
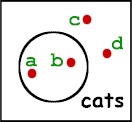
However, even with this new notation, there are still other pieces of information that cannot be represented, such as :
- Either Felix is a cat or it is a dog.
- If Peter is taller than Mary then Peter is older than Mary.
Perhaps it might be possible to introduce additional new symbols to represent such ideas. But then the system of Venn diagrams will get really complicated and difficult to use. So now that we know the limitations of Venn diagrams, we should be in a better position to know when they are useful and when they are not.
- See if you can invent a new notation for representing a sentence such as "Felix is either a cat or a dog.".
- This is a difficult question. How would you draw a Venn diagram to represent the relationships between five sets of objects? One possible answer can be found on Wikipedia here.